这样 (2,4)-环面链环 的两条曲线的环绕数是 4。 在数学 中,环绕数 (linking number )是描述三维空间 中两条闭曲线 环绕的一个数值不变量 。直观上,环绕数表示每一条曲线缠绕另一条曲线的次数。环绕数总是整数 ,但有可能取正数或负数,取决于这两条曲线的定向 。
环绕数由高斯 以环绕积分 的形式引入。它在纽结理论 、代数拓扑 和微分几何 的研究中是重要的对象,并在数学 和科学 中有许多应用,包括量子力学 、电磁学 以及 DNA超螺旋 的研究。
空间中任何两条闭曲线都恰好可以移动 成如下标准位置之一。这决定了环绕数:
⋯
{\displaystyle \cdots }
环绕数 -2
环绕数 -1
环绕数 0
⋯
{\displaystyle \cdots }
环绕数 1
环绕数 2
环绕数 3
每条曲线在移动过程中可以穿过自身,但这两条曲线保持互相分离。
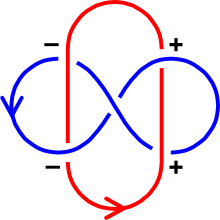
六个正交叉与两个负交叉,这两条曲线的环绕数为 2。 存在一个算法计算出一个链环图表 的环绕数。按如下法则将每个交叉标记为“正”或“负”
[ 1]
正交叉数总数减去负交叉数总数等于环绕数的两倍,即
环绕数
=
n
1
+
n
2
−
n
3
−
n
4
2
,
{\displaystyle ={\frac {n_{1}+n_{2}-n_{3}-n_{4}}{2}},\,}
这里 n 1 , n 2 , n 3 , n 4 分别表示四类交叉数的个数。两个和
n
1
+
n
3
{\displaystyle n_{1}+n_{3}\,\!}
n
2
+
n
4
{\displaystyle n_{2}+n_{4}\,\!}
[ 2]
环绕数
=
n
1
−
n
4
=
n
2
−
n
3
.
{\displaystyle =\,n_{1}-n_{4}\,=\,n_{2}-n_{3}.\,}
注意到
n
1
−
n
4
{\displaystyle n_{1}-n_{4}}
n
2
−
n
3
{\displaystyle n_{2}-n_{3}}
怀特黑德链环两条曲线环绕数为零。 任何两条没有链接起来的曲线相交数为零。但环绕数为零的两条曲线仍可能是链接起来的(例如右图的怀特黑德链环
逆转任何一条曲线的定向,环绕数改变符号;但两条曲线同时逆转定向,环绕数不变。
环绕数具有手征性 :取一个链环的镜像 ,环绕数改变符号。我们对正环绕数的约定基于右手法则 。
x -y 平面上一条定向曲线的卷绕数 等于它与 z -轴(将 z -轴想象为三维球面 中一条闭曲线)的环绕数。更一般地,如果其中一条曲线是简单 的,则这个分支的第一同调群 同构于整数 Z 。在此情形,环绕数由另一条曲线的同调类决定。
在物理学 中,环绕数是拓扑量子数 之一例,它与量子纠缠 有关。 给定两条不交可微曲线
γ
1
,
γ
2
:
S
1
→
R
3
{\displaystyle \gamma _{1},\gamma _{2}\colon S^{1}\rightarrow \mathbb {R} ^{3}}
环面 到单位球面 高斯映射
Γ
{\displaystyle \Gamma }
Γ
(
s
,
t
)
=
γ
1
(
s
)
−
γ
2
(
t
)
|
γ
1
(
s
)
−
γ
2
(
t
)
|
.
{\displaystyle \Gamma (s,t)={\frac {\gamma _{1}(s)-\gamma _{2}(t)}{|\gamma _{1}(s)-\gamma _{2}(t)|}}.\,}
取单位球面上一点 v ,从而链环的正交投影到垂直于 v 的平面给出一个链环图表。观察到点 (s , t ) 在高斯映射下映为 v 对应于链环图表中一个交叉,这里
γ
1
{\displaystyle \gamma _{1}}
γ
2
{\displaystyle \gamma _{2}}
s , t ) 的一个邻域在高斯映射下映为 v 的一个邻域,保持或逆转定向取决于交叉的符号。从而为了计算这个对应于 v 的链环图表的环绕数,只需数高斯映射覆盖 v 的带符号次数。由于 v 是一个正则值 ,这恰是高斯映射的度数 (即 Γ 的像 盖住球面的带符号次数)。环绕数的同痕 不变性自动由度数在同伦下不变得到。任何其它正则值将得到相同的数,所以环绕数与任何特定的链环图表无关。
曲线 γ 1 与 γ 2 的环绕数的这种表述给出了用二重线积分 表示的一个明确公式,即高斯 环绕积分
环绕数
=
ϕ
(
γ
1
,
γ
2
)
=
1
4
π
∮
γ
1
∮
γ
2
r
1
−
r
2
|
r
1
−
r
2
|
3
⋅
(
d
r
1
×
d
r
2
)
.
{\displaystyle {}\,=\,\phi (\gamma _{1},\gamma _{2})={\frac {1}{4\pi }}\oint _{\gamma _{1}}\oint _{\gamma _{2}}{\frac {\mathbf {r} _{1}-\mathbf {r} _{2}}{|\mathbf {r} _{1}-\mathbf {r} _{2}|^{3}}}\cdot (d\mathbf {r} _{1}\times d\mathbf {r} _{2}).}
这个积分求出了高斯映射像的全部带符号面积(被积函数是 Γ 的雅可比矩阵 ),然后除以球面的面积(等于 4π)。
就像三维中环绕 的闭曲线,任何两个维数为 m 与 n 的闭流形 ,可能在
m
+
n
+
1
{\displaystyle m+n+1}
欧几里得空间 中环绕起来。任何这样链环有一个相伴的高斯映射,其度数 是环绕数的推广。
任何标架纽结 自环绕数 ,得自计算纽结 C 与将曲线 C 中的点沿着标架向量稍微移动得到一条新曲线的环绕数。由铅直移动(沿着黑板标架)得到的自环绕数称为考夫曼自环绕数 (Kauffman's self-linking number )。 U(1) 陳-西蒙斯理論 是:
C
S
=
k
4
π
∫
M
A
d
A
{\displaystyle CS={\frac {k}{4\pi }}\int _{M}AdA}
若
M
=
R
3
{\displaystyle M=R^{3}}
路徑積分 是
Z
(
C
1
,
C
2
)
=
∫
d
A
exp
(
i
C
S
+
i
∫
C
1
A
+
i
∫
C
2
A
)
=
∫
d
A
exp
(
i
C
S
+
i
∫
J
A
)
{\displaystyle Z(C_{1},C_{2})=\int dA\exp {(iCS+i\int _{C_{1}}A+i\int _{C_{2}}A)}=\int dA\exp {(iCS+i\int JA)}}
包括C1和C2的威爾森迴圈 。J=J1+J2,而且
J
i
a
=
∫
C
i
d
x
a
δ
3
(
x
−
x
i
(
t
)
)
{\displaystyle J_{i}^{a}=\int _{C_{i}}dx^{a}\delta ^{3}(x-x_{i}(t))}
因為這是高斯的積分,所以我們不需要重整化 或正規化 。再說這個積分是拓撲不變。
若J是经典方程就是
d
A
=
(
2
π
/
k
)
∗
J
{\displaystyle dA=(2\pi /k)*J}
或
∇
×
A
=
2
π
J
/
k
{\displaystyle \nabla \times A=2\pi J/k}
若我们选洛伦茨规范
d
∗
A
=
0
{\displaystyle d*A=0}
∇
2
A
=
−
2
π
∇
×
J
/
k
{\displaystyle \nabla ^{2}A=-2\pi \nabla \times J/k}
从电磁学 ,解是
A
(
x
)
=
1
2
k
∫
d
3
y
∇
×
J
(
y
)
|
x
−
y
|
{\displaystyle A(x)={\frac {1}{2k}}\int d^{3}y{\frac {\nabla \times J(y)}{|x-y|}}}
则
Z
[
C
1
,
C
2
]
=
exp
(
2
π
i
ϕ
(
C
1
,
C
2
)
/
k
)
{\displaystyle Z[C_{1},C_{2}]=\exp(2\pi i\phi (C_{1},C_{2})/k)}
这是最简单的一个拓撲量子場論 。根据爱德华·威滕 的证明,非阿贝尔G的陈-西蒙斯论给其他拓扑不变,例如琼斯多项式 。
^ 这与计算一个纽结 的绞拧数 时使用的标记是一致的,不过此情形我们只需标记涉及两条曲线的交叉。
^ 如果其中一条曲线是简单的,这由若尔当曲线定理 得到。例如,如果蓝曲线是简单的,则 n 1 + n 3 与 n 2 + n 4
表示红曲线向内与向外穿过蓝曲线所围区域的次数。
A.V. Chernavskii, Linking coefficient , Hazewinkel, Michiel (编), 数学百科全书 , Springer , 2001, ISBN 978-1-55608-010-4 -, Writhing number , Hazewinkel, Michiel (编), 数学百科全书 , Springer , 2001, ISBN 978-1-55608-010-4 
































![{\displaystyle Z[C_{1},C_{2}]=\exp(2\pi i\phi (C_{1},C_{2})/k)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39d5041f7d71e957a5bfa90c144f034ff613ee6b)