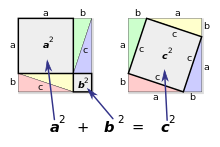
直角边 的平方和等于斜边 的平方勾股定理 (英语:Pythagorean theorem / Pythagoras' theorem )是平面几何 中一个基本而重要的定理 。勾股定理说明,平面 上的直角三角形 的两条直角边的长度(较短直角边古称勾长、较长直角边古称股长)的平方 和等于斜边长(古称弦长)的平方。反之,若平面上三角形中两边长的平方和等于第三边边长的平方,则它是直角三角形(直角所对的边是第三边)。勾股定理是人类早期发现并证明的重要数学定理之一。
此定理又称毕氏定理 、商高定理 、毕达哥拉斯定理 、新娘座椅定理 或百牛定理 。“毕氏”所指的是其中一个发现这个定理的古希腊数学家毕达哥拉斯 ,但历史学家相信这个定理早在毕达哥拉斯出生的一千年前已经在世界各地广泛应用。不过,现代西方数学界统一称呼它为“毕达哥拉斯定理”。日本除了翻译西方的“毕达哥拉斯之定理”外亦有“三平方之定理”的称呼。
早在有明文描述此定理前,古埃及 在公元前 1600年的纸莎草 记载有
(
3
,
4
,
5
)
{\displaystyle (3,4,5)}
勾股数 ,而古巴比伦 泥板纪录的最大的一个勾股数组是
(
12709
,
13500
,
18541
)
{\displaystyle (12709,13500,18541)}
现在勾股定理可考的严谨数学证明,起源于略晚于毕德格拉斯的欧几里得 几何原本 中,卷一命题47。但奇怪的是,这个定理从未被叫做“欧几里得定理”。
《周髀算经 》中,用商高 与周公 对谈的方式,提出
(
3
,
4
,
5
)
{\displaystyle (3,4,5)}
[ 1] [ 2]
有些参考资料提到法国和比利时将勾股定理称为驴桥定理 ,但驴桥定理是指等腰三角形 的二底角相等,非勾股定理[ 3]
勾股定理有四百多个证明,如微分证明,面积证明等。
在平面上的一个直角三角形中,两个直角边边长的平方加起来等于斜边长的平方。如果设直角三角形的两条直角边长度分别是
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
或
a
2
+
b
2
=
c
{\displaystyle {\sqrt {a^{2}+b^{2}}}=c}
余弦定理 是勾股定理的一个推广[ 4] 证明 方法,是数学定理 中证明方法最多的定理之一[ 5]
如果
c
{\displaystyle c}
长度 而
a
{\displaystyle a}
b
{\displaystyle b}
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}\,}
如果
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
c
=
a
2
+
b
2
.
{\displaystyle c={\sqrt {a^{2}+b^{2}}}.\,}
如果斜边的长度
c
{\displaystyle c}
a
{\displaystyle a}
b
{\displaystyle b}
a
=
c
2
−
b
2
.
{\displaystyle a={\sqrt {c^{2}-b^{2}}}.\,}
或
b
=
c
2
−
a
2
.
{\displaystyle b={\sqrt {c^{2}-a^{2}}}.\,}
简单来说,只要知道直角三角形的其中两条边长,便能求出第三条边长。
勾股数组 是满足勾股定理
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}}
正整数 组
(
a
,
b
,
c
)
{\displaystyle (a,b,c)}
a
,
b
,
c
{\displaystyle a,b,c}
勾股数 。例如
(
3
,
4
,
5
)
{\displaystyle (3,4,5)}
任意一组勾股数
(
a
,
b
,
c
)
{\displaystyle (a,b,c)}
a
=
k
(
m
2
−
n
2
)
,
b
=
2
k
m
n
,
c
=
k
(
m
2
+
n
2
)
{\displaystyle a=k(m^{2}-n^{2}),b=2kmn,c=k(m^{2}+n^{2})}
k
,
m
,
n
∈
N
∗
,
m
>
n
{\displaystyle k,m,n\in \mathbb {N*} ,m>n}
公元前18世纪记录各种勾股数组的巴比伦石板 这个定理的历史可以被分成三个部分:发现勾股数 、发现直角三角形 中边长的关系、及其定理的证明。
勾股数的发现时间较早,例如埃及的纸草书里面就有
(
3
,
4
,
5
)
{\displaystyle (3,4,5)}
(
13500
,
12709
,
18541
)
{\displaystyle (13500,12709,18541)}
[ 6] 周髀算经 》中也记述了
(
3
,
4
,
5
)
{\displaystyle (3,4,5)}
[ 7] 金朝 数学家李冶 在《测圆海镜 》中,通过勾股容圆 图式的十五个勾股形和直径的关系,建立了系统的天元术 ,推导出692条关于勾股形的各边的公式,其中用到了多组勾股数作为例子。
巴比伦人得到的勾股数的数量和质量不太可能纯从测量手段获得。之后的毕达哥拉斯 本人并无著作传世,不过在他死后一千年,5世纪的普罗克勒斯 给欧几里德 的名著《几何原本 》做注解时将最早的发现和证明归功于毕达哥拉斯学派 :
“
如果我们听听那些喜欢说古代历史的人,他们把这个定理归于毕达哥拉斯,并且说他杀了一百头公牛来庆祝。对我来说,虽然我欣赏那个第一个观察到这个定理的人,我更叹服《原本》的作者。不光是因为他给出了清晰明确的证明,而且还因为他用无可置疑的方法在第六篇中证明了一个更一般的命题。
”
普鲁塔克 和西塞罗 也将发现的功劳归于毕达哥拉斯,但没有任何证据表明毕达哥拉斯证明了勾股定理,以素食 闻名的毕达哥拉斯杀牛更是不可思议。
在中国,记载秦朝的算数书 并未记载勾股定理,只是记录了一些勾股数。定理首次载于书面则是在成书于西汉但内容收集整理自公元前一千多年以来的《周髀算经 》“荣方问于陈子”一节中:
“
若求邪至日者,以日下为勾,日高为股,勾股各自乘,并而开方除之,得邪至日。
”
——《周髀算经 》卷上之二
因此此定理也被称之为陈子定理。
东汉末年赵爽 《周髀算经 注》《勾股圆方图注》记载:
“
勾股各自乘,并之,为弦实,开方除之,即弦。
”
赵爽 《勾股圆方图》在《九章算术 注》中,刘徽 反复利用勾股定理求圆周率 ,并利用“割补术”做“青朱出入图 ”完成勾股定理的几何图形证明。
直至现时为止,仍有许多关于勾股定理是否不止一次被发现的辩论。
毕达哥拉斯学派的证明没有流传下来,流传下来书面证明最早见于《几何原本》第一册的第47个命题。在中国,东汉末年吴国的赵爽 最早给出勾股定理的证明。巴勒蒂·克尔什纳·蒂尔特吉 吠陀数学 一书中声称古代印度教吠陀证明了勾股定理。
这个定理有许多证明的方法,其证明的方法可能是数学众多定理中最多的。路明思(Elisha Scott Loomis)的Pythagorean Proposition 一书中总共提到367种证明方式。
有人会尝试以三角恒等式 (例如:正弦 和余弦 函数的泰勒级数 )来证明勾股定理,但是,因为所有的基本三角恒等式都是建基于勾股定理,所以不能作为勾股定理的证明(参见循环论证 )。
中国三国 时期赵爽 为证明勾股定理作“勾股圆方图”即“弦图”,按其证明思路,其法可涵盖所有直角三角形,为东方特色勾股定理无字证明法。2002年第24届国际数学家大会 (ICM)在北京 召开。中国邮政 发行一枚邮资明信片,邮资图就是这次大会的会标—中国古代证明勾股定理的赵爽弦图。
赵爽 勾股圆方图证明勾股定理法动画 中国魏晋 时期数学家刘徽 依据其“割补术”为证勾股定理另辟蹊径而作“青朱出入图 ”。刘徽描述此图,“勾自乘为朱方,股自乘为青方,令出入相补,各从其类,因就其余不动也,合成弦方之幂。开方除之,即弦也。[ 8]
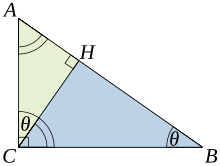
刘徽 青朱出入图 相似三角形的证明 有许多勾股定理的证明方式,都是基于相似 三角形中两边长的比例 。
设
A
B
C
{\displaystyle ABC}
∠
C
{\displaystyle \angle C}
C
{\displaystyle C}
高 ,并将此高与
A
B
¯
{\displaystyle {\overline {AB}}}
H
{\displaystyle H}
△
A
C
H
{\displaystyle \bigtriangleup ACH}
△
A
B
C
{\displaystyle \bigtriangleup ABC}
A
{\displaystyle A}
△
C
B
H
{\displaystyle \bigtriangleup CBH}
△
A
B
C
{\displaystyle \bigtriangleup ABC}
因为
B
C
¯
=
a
,
A
C
¯
=
b
,
and
A
B
¯
=
c
,
{\displaystyle {\overline {BC}}=a,{\overline {AC}}=b,{\text{ and }}{\overline {AB}}=c,\!}
所以
a
c
=
H
B
¯
a
and
b
c
=
A
H
¯
b
.
{\displaystyle {\frac {a}{c}}={\frac {\overline {HB}}{a}}{\text{ and }}{\frac {b}{c}}={\frac {\overline {AH}}{b}}.\,}
可以写成
a
2
=
c
×
H
B
¯
and
b
2
=
c
×
A
H
¯
.
{\displaystyle a^{2}=c\times {\overline {HB}}{\text{ and }}b^{2}=c\times {\overline {AH}}.\,}
综合这两个方程式,我们得到
a
2
+
b
2
=
c
×
H
B
¯
+
c
×
A
H
¯
=
c
×
(
H
B
¯
+
A
H
¯
)
=
c
2
.
{\displaystyle a^{2}+b^{2}=c\times {\overline {HB}}+c\times {\overline {AH}}=c\times ({\overline {HB}}+{\overline {AH}})=c^{2}.\,\!}
换句话说:
a
2
+
b
2
=
c
2
.
{\displaystyle a^{2}+b^{2}=c^{2}.\,\!}
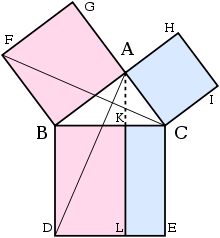
《几何原本》中的证明 在欧几里得 的《几何原本 》一书中给出勾股定理的以下证明。设
△
A
B
C
{\displaystyle \bigtriangleup ABC}
A 为直角。从
A
{\displaystyle A}
在定理的证明中,我们需要如下四个辅助定理:
如果两个三角形有两组对应边和这两组边所夹的角相等,则两三角形全等。(SAS定理)
三角形面积是任一同底同高之平行四边形面积的一半。
任意一个正方形的面积等于其二边长的乘积。
任意一个矩形的面积等于其二边长的乘积(据辅助定理3)。 证明的思路为:把上方的两个正方形,透过等高同底的三角形,以其面积关系,变换成下方两个同等面积的长方形。
证明辅助图2 其证明如下:
设
△
A
B
C
{\displaystyle \triangle ABC}
∠
C
A
B
{\displaystyle \angle CAB}
其边为
B
C
¯
{\displaystyle {\overline {BC}}}
A
B
¯
{\displaystyle {\overline {AB}}}
C
A
¯
{\displaystyle {\overline {CA}}}
C
B
D
E
{\displaystyle CBDE}
B
A
G
F
{\displaystyle BAGF}
A
C
I
H
{\displaystyle ACIH}
画出过点
A
{\displaystyle A}
B
D
¯
{\displaystyle {\overline {BD}}}
C
E
¯
{\displaystyle {\overline {CE}}}
B
C
¯
{\displaystyle {\overline {BC}}}
D
E
¯
{\displaystyle {\overline {DE}}}
K
{\displaystyle K}
L
{\displaystyle L}
分别连接
C
F
¯
{\displaystyle {\overline {CF}}}
A
D
¯
{\displaystyle {\overline {AD}}}
B
C
F
{\displaystyle BCF}
B
D
A
{\displaystyle BDA}
∠
C
A
B
{\displaystyle \angle CAB}
∠
B
A
G
{\displaystyle \angle BAG}
C
{\displaystyle C}
A
{\displaystyle A}
G
{\displaystyle G}
B
{\displaystyle B}
A
{\displaystyle A}
H
{\displaystyle H}
∠
C
B
D
{\displaystyle \angle CBD}
∠
F
B
A
{\displaystyle \angle FBA}
∠
A
B
D
{\displaystyle \angle ABD}
∠
F
B
C
{\displaystyle \angle FBC}
因为
A
B
¯
{\displaystyle {\overline {AB}}}
B
D
¯
{\displaystyle {\overline {BD}}}
F
B
¯
{\displaystyle {\overline {FB}}}
B
C
¯
{\displaystyle {\overline {BC}}}
△
A
B
D
{\displaystyle \triangle ABD}
△
F
B
C
{\displaystyle \triangle FBC}
因为
A
{\displaystyle A}
K
{\displaystyle K}
L
{\displaystyle L}
B
D
L
K
{\displaystyle BDLK}
△
A
B
D
{\displaystyle \triangle ABD}
因为
C
{\displaystyle C}
A
{\displaystyle A}
G
{\displaystyle G}
B
A
G
F
{\displaystyle BAGF}
△
F
B
C
{\displaystyle \triangle FBC}
因此四边形
B
D
L
K
{\displaystyle BDLK}
B
A
G
F
{\displaystyle BAGF}
A
B
¯
2
{\displaystyle {\overline {AB}}^{2}}
同理可证,四边形
C
K
L
E
{\displaystyle CKLE}
A
C
I
H
=
A
C
¯
2
{\displaystyle ACIH={\overline {AC}}^{2}}
把这两个结果相加,
A
B
¯
2
+
A
C
¯
2
=
B
D
¯
×
B
K
¯
+
K
L
¯
×
K
C
¯
{\displaystyle {\overline {AB}}^{2}+{\overline {AC}}^{2}={\overline {BD}}\times {\overline {BK}}+{\overline {KL}}\times {\overline {KC}}}
由于
B
D
¯
=
K
L
¯
{\displaystyle {\overline {BD}}={\overline {KL}}}
B
D
¯
×
B
K
¯
+
K
L
¯
×
K
C
¯
=
B
D
¯
(
B
K
¯
+
K
C
¯
)
=
B
D
¯
×
B
C
¯
{\displaystyle {\overline {BD}}\times {\overline {BK}}+{\overline {KL}}\times {\overline {KC}}={\overline {BD}}\left({\overline {BK}}+{\overline {KC}}\right)={\overline {BD}}\times {\overline {BC}}}
由于
C
B
D
E
{\displaystyle CBDE}
A
B
¯
2
+
A
C
¯
2
=
B
C
¯
2
{\displaystyle {\overline {AB}}^{2}+{\overline {AC}}^{2}={\overline {BC}}^{2}}
此证明是于欧几里得 《几何原本 》一书第1.47节所提出的[ 9]
由于这个定理的证明依赖于平行公理,而且从这个定理可以推出平行公理,很多人质疑平行公理是这个定理的必要条件,一直到十九世纪尝试否定第五公理的非欧几何 出现。
以面积减算法证明 此证明以图形重新排列证明。两个大正方形的面积皆为
(
a
+
b
)
2
{\displaystyle (a+b)^{2}}
a
2
+
b
2
{\displaystyle a^{2}+b^{2}}
c
2
{\displaystyle c^{2}}
以重新排列法证明
以动画方式来论证勾股定理 勾股定理的逆定理是判断三角形为钝角、锐角或直角的一个简单的方法,其中
A
B
¯
=
c
{\displaystyle {\overline {AB}}=c}
如果
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}\,}
△
A
B
C
{\displaystyle \triangle ABC}
∠
C
{\displaystyle \angle C}
如果
a
2
+
b
2
>
c
2
{\displaystyle a^{2}+b^{2}>c^{2}\,}
△
A
B
C
{\displaystyle \triangle ABC}
A
B
¯
=
c
{\displaystyle {\overline {AB}}=c}
∠
C
{\displaystyle \angle C}
如果
a
2
+
b
2
<
c
2
{\displaystyle a^{2}+b^{2}<c^{2}\,}
△
A
B
C
{\displaystyle \triangle ABC}
∠
C
{\displaystyle \angle C}
(这个逆定理其实只是余弦定理 的一个延伸)
勾股定理的逆定理的证法数明显少于勾股定理的证法。以下是一些常见证法。
构造
△
A
′
B
′
C
′
{\displaystyle \triangle A'B'C'}
a
′
=
a
,
b
′
=
b
,
∠
C
′
=
90
∘
{\displaystyle a'=a,b'=b,\angle C'=90^{\circ }}
根据勾股定理,
c
′
=
a
′
2
+
b
′
2
=
a
2
+
b
2
=
c
{\displaystyle c'={\sqrt {a'^{2}+b'^{2}}}={\sqrt {a^{2}+b^{2}}}=c}
△
A
′
B
′
C
′
≅
△
A
B
C
(
S
S
S
)
{\displaystyle \triangle A'B'C'\cong \triangle ABC(SSS)}
因此,
∠
C
=
90
∘
{\displaystyle \angle C=90^{\circ }}
根据余弦定理,
cos
C
=
a
2
+
b
2
−
c
2
2
a
b
{\displaystyle \cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}}
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}\,}
cos
C
=
0
{\displaystyle \cos C=0\,}
∠
C
=
90
∘
{\displaystyle \angle C=90^{\circ }}
在
A
B
¯
{\displaystyle {\overline {AB}}}
D
{\displaystyle D}
∠
D
C
B
=
∠
A
{\displaystyle \angle DCB=\angle A}
在
△
C
D
B
{\displaystyle \triangle CDB\,}
△
A
C
B
{\displaystyle \triangle ACB\,}
∠
B
=
∠
B
,
∠
D
C
B
=
∠
A
⇒
△
C
D
B
∼
△
A
C
B
{\displaystyle \angle B=\angle B,\angle DCB=\angle A\Rightarrow \triangle CDB\sim \triangle ACB}
。
从而,
B
C
¯
B
A
¯
=
B
D
¯
B
C
¯
⇒
B
D
¯
=
a
2
c
{\displaystyle {\frac {\overline {BC}}{\overline {BA}}}={\frac {\overline {BD}}{\overline {BC}}}\Rightarrow {\overline {BD}}={\frac {a^{2}}{c}}}
C
D
¯
A
C
¯
=
C
B
¯
A
B
¯
⇒
C
D
¯
=
a
b
¯
c
{\displaystyle {\frac {\overline {CD}}{\overline {AC}}}={\frac {\overline {CB}}{\overline {AB}}}\Rightarrow {\overline {CD}}={\frac {\overline {ab}}{c}}}
另一方面,
A
D
¯
=
A
B
¯
−
B
D
¯
=
c
−
a
2
c
=
b
2
c
{\displaystyle {\overline {AD}}={\overline {AB}}-{\overline {BD}}=c-{\frac {a^{2}}{c}}={\frac {b^{2}}{c}}}
D
C
¯
A
D
¯
=
B
C
¯
A
C
¯
=
B
D
¯
C
D
¯
=
a
b
{\displaystyle {\frac {\overline {DC}}{\overline {AD}}}={\frac {\overline {BC}}{\overline {AC}}}={\frac {\overline {BD}}{\overline {CD}}}={\frac {a}{b}}}
△
A
C
D
∼
△
C
B
D
{\displaystyle \triangle ACD\sim \triangle CBD}
因而,
∠
B
D
C
=
∠
C
D
A
=
90
∘
{\displaystyle \angle BDC=\angle CDA=90^{\circ }}
∠
A
C
B
=
∠
C
D
B
=
90
∘
{\displaystyle \angle ACB=\angle CDB=90^{\circ }}
勾股定理是由欧几里得几何 的公理推导出来的,其在非欧几里得几何中不成立的[ 10] 平行公设 。[ 11] [ 12]