使用者:Subgradient/葛羅佛算法

Grover算法 是一種 量子算法 ；它只需要執行$O({\sqrt {N}})$次某個黑盒函數，就能以很高的概率的概率找到使黑盒函數找到產生某個特定輸出的輸入（$N$是黑盒函數的定義域大小）。它由 Lov Grover 在1996年提出。

經典計算機不能在不到 $O(N)$次執行內解決類似的問題（因為在最壞的情況中，第N個定義域的成員才是正確的解）。在Grover發表算法的大約同一時間，Bennett，Bernstein，Brasard以及Vazirani證明了，沒有量子算法可以在 ${\displaystyle }$ 次執行內解決這個問題；因此Grover算法是 漸進的最佳的。

已經證明，非局域隱變量的量子計算機可以用至多 ${\displaystyle O({\sqrt[{3}]{N}})}$步實現對有$N$個元素的資料庫的搜索。 這比Grover算法所需要的 ${\displaystyle }$ 步要快。

以上兩種搜索方法都不能讓量子計算機在多項式時間內解決 NP完全 的問題。 不同於其他的可以提供指數加速的量子算法，Grover的算法，只提供了平方級別的加速。 然而，即使是平方的加速在 ${\displaystyle }$ 很大的時候也足夠大。 Grover的算法，可以在大約$2^{64}$次迭代內 暴力破解 128位的對稱加密密鑰，或者在大約$2^{128}$ 迭代內破解256位密鑰。 因此，有人建議 將對稱密鑰長度增加一倍，以防範未來的量子攻擊。

應用

雖然Grover的算法的目的通常被描述為"搜索資料庫"，但更準確地說，它應該被描述為"求函數的逆"。 大致說來，如果我們有一個可以在量子計算機上求值的函數 ${\displaystyle }$ ，Grover的算法可以在給定 <math>y</math> 時計算 ${\displaystyle }$ 。對函數求逆和資料庫搜索有關，因為我們可以構造一個函數，如果 ${\displaystyle }$ 匹配資料庫中的一個所需項目，產生一個特定的值 y (比如"真")；而對於其它的 x，返回另一個值 ${\displaystyle }$ ("假")。

Grover的算法還可用於估計一組數的 平均 和 中位數 ，以及解決 碰撞問題的。 如果有多個匹配的條目且數量事先知道，這一算法還可進一步優化。 Grover的算法也可以用於破解密碼。

設定

考慮一個擁有 N 個條目的無序資料庫。 算法需要一個 N-維 態空間 H；這可以用 n =log₂ N 個 量子比特 提供。考慮這樣一個問題：尋找滿足某些標準的資料庫條目的索引。 讓 f 是一個將資料庫條目映為0或1的函數，且 f(x)=1若且唯若 x 滿足搜索標準(x = ω)。我們可以(以量子黑盒的形式)使用一個 么正算子 U_ω ，其作用為：

${\displaystyle }$

 U_ω 的另外一種定義如下。假定存在一個 輔助量子比特 系統(如下圖中的量子電路所描繪的)。 那麼，這個算子表示有受主系統中 f(x)的值控制的受控非(非 門)：

${\displaystyle }$

更加簡短地，

${\displaystyle }$

這是一種利用 去計算方法來實現一個二元運算的自然的方法。 需要注意的是，如果輔助量子比特初始狀態為 ${\displaystyle }$門將等效於上文中的操作，同時輔助系統不再與主系統糾纏：

$U_{\omega }{\big (}|x\rangle \otimes |-\rangle {\big )}={\frac {1}{\sqrt {2}}}\left(U_{\omega }|x\rangle |0\rangle -U_{\omega }|x\rangle |1\rangle \right)={\frac {1}{\sqrt {2}}}\left(|x\rangle |f(x)\rangle -|x\rangle |1\oplus f(x)\rangle \right)={\begin{cases}{\frac {1}{\sqrt {2}}}\left(|x\rangle |1\rangle -|x\rangle |0\rangle \right)=-|x\rangle \otimes |-\rangle &{\text{if }}f(x)=1,\\{\frac {1}{\sqrt {2}}}\left(|x\rangle |0\rangle -|x\rangle |1\rangle \right)=|x\rangle \otimes |-\rangle &{\text{if }}f(x)=0\end{cases}}$

在以上兩種設定中，我們的目標都是尋找 ${\displaystyle }$。

算法的步驟

表示Grover算法的量子電路

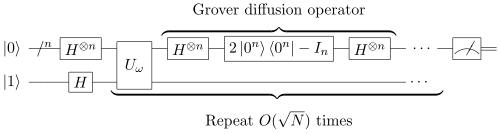
Grover算法的步驟如下。 讓$|s\rangle$表示所有狀態的均勻疊加態

$|s\rangle ={\frac {1}{\sqrt {N}}}\sum _{x=0}^{N-1}|x\rangle .$

那麼算子

$U_{s}=2\left|s\right\rangle \left\langle s\right|-I$

記為Grover擴散算子。

以下是算法：

1. 將系統初始化為
   $|s\rangle ={\frac {1}{\sqrt {N}}}\sum _{x=0}^{N-1}|x\rangle$。
2. 執行以下"Grover迭代" r(N)次。 函數 r(N)（漸近 O(N^1/2)）將在下文中說明。
   1. 作用算子$U_{\omega }$。
   2. 作用算子$U_{s}$。
3. 執行測量Ω。 測量 的結果將以接近1的概率（在N ≫ 1時）是本徵值 λ_ω 。ω 可以從λ_ω求得。

參見

• 幅度放大
• 秀爾算法
• 德布羅意–波姆理論

參考文獻

• Grover L.K.: A fast quantum mechanical algorithm for database search, Proceedings, 28th Annual ACM Symposium on the Theory of Computing, (May 1996) p. 212
• Grover L.K.: From Schrödinger's equation to quantum search algorithm, American Journal of Physics, 69(7): 769-777, 2001. Pedagogical review of the algorithm and its history.
• Grover L.K.: QUANTUM COMPUTING: How the weird logic of the subatomic world could make it possible for machines to calculate millions of times faster than they do today The Sciences, July/August 1999, pp. 24–30.
• Nielsen, M.A. and Chuang, I.L. Quantum computation and quantum information. Cambridge University Press, 2000. Chapter 6.
• What's a Quantum Phone Book?, Lov Grover, Lucent Technologies
• Grover's Algorithm: Quantum Database Search, C. Lavor, L.R.U. Manssur, R. Portugal
• Grover's algorithm on arxiv.org

外部連結

• Davy Wybiral. Quantum Circuit Simulator. |author=和|last=只需其一 (幫助)
• Craig Gidney. Grover’s Quantum Search Algorithm. 2013-03-05. |author=和|last=只需其一 (幫助)
• François Schwarzentruber. Grover's algorithm. 2013-05-18. |author=和|last=只需其一 (幫助)
• Alexander Prokopenya. Quantum Circuit Implementing Grover's Search Algorithm. Wolfram Alpha. |author=和|last=只需其一 (幫助)

舉web

URL

https://web.eecs.umich.edu/~imarkov/pubs/jour/cise05-grov的。pdf

標題

是量子搜索實用？

最後一名

亞歷山大Prokopenya

今年的出版物

2005年

出版商

Wolfram阿爾法

網頁

案62-70中

DOI

10.1109/認證的。2005年。53

[[Category:量子演算法]] [[Category:搜尋演算法]]