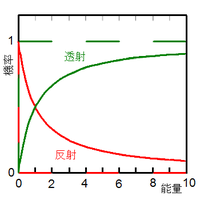
對於一個Delta位勢阱的散射 。往左與往右的行進波 的振幅與方向都分別表示於圖內。用來計算透射係數 與反射係數 的行進波 都以紅色表示。 在量子力學 裏,Delta位勢阱 是一個阱 內位勢為負狄拉克Delta函數 ,阱外位勢為0的位勢阱。Delta位勢阱問題 專門研討,在這種位勢的作用中,一個粒子的量子行為。這是一個常見的理論問題。假若,粒子的能量是正值的,我們想要知道的是,在被Delta位勢壘散射 的狀況下,粒子的反射係數 與透射係數 。假若,粒子的能量是負值的,這粒子會被束縛於Delta位勢阱的阱內。這時,我們想要知道的是粒子的能量與束縛的量子態。
一個粒子獨立於時間 的薛丁格方程式 為
−
ℏ
2
2
m
d
2
ψ
(
x
)
d
x
2
+
V
(
x
)
ψ
(
x
)
=
E
ψ
(
x
)
{\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi (x)}{dx^{2}}}+V(x)\psi (x)=E\psi (x)\,\!}
其中,
ℏ
{\displaystyle \hbar \,\!}
約化普朗克常數 ,
m
{\displaystyle m\,\!}
x
{\displaystyle x\,\!}
E
{\displaystyle E\,\!}
ψ
(
x
)
{\displaystyle \psi (x)\,\!}
波函數 ,
V
(
x
)
{\displaystyle V(x)\,\!}
V
(
x
)
=
−
λ
δ
(
x
)
{\displaystyle V(x)=-\lambda \delta (x)\,\!}
其中,
δ
(
x
)
{\displaystyle \delta (x)\,\!}
狄拉克Delta函數 ,
λ
{\displaystyle \lambda \,\!}
這位勢阱將一維空間分為兩個區域:
x
<
0
{\displaystyle x<0\,\!}
x
>
0
{\displaystyle x>0\,\!}
疊加 (參閱自由粒子 ):
ψ
L
(
x
)
=
A
r
e
i
k
x
+
A
l
e
−
i
k
x
x
<
0
{\displaystyle \psi _{L}(x)=A_{r}e^{ikx}+A_{l}e^{-ikx}\quad x<0\,\!}
ψ
R
(
x
)
=
B
r
e
i
k
x
+
B
l
e
−
i
k
x
x
>
0
{\displaystyle \psi _{R}(x)=B_{r}e^{ikx}+B_{l}e^{-ikx}\quad x>0\,\!}
其中,
A
r
{\displaystyle A_{r}\,\!}
A
l
{\displaystyle A_{l}\,\!}
B
r
{\displaystyle B_{r}\,\!}
B
l
{\displaystyle B_{l}\,\!}
邊界條件 決定的常數,下標
r
{\displaystyle r\,\!}
l
{\displaystyle l\,\!}
k
=
2
m
E
/
ℏ
2
{\displaystyle k={\sqrt {2mE/\hbar ^{2}}}\,\!}
波數 。
當
E
>
0
{\displaystyle E>0\,\!}
ψ
L
{\displaystyle \psi _{L}\,\!}
ψ
R
{\displaystyle \psi _{R}\,\!}
行進波 。可是,當
E
<
0
{\displaystyle E<0\,\!}
ψ
L
{\displaystyle \psi _{L}\,\!}
ψ
R
{\displaystyle \psi _{R}\,\!}
x
{\displaystyle x\,\!}
在
x
=
0
{\displaystyle x=0\,\!}
ψ
L
=
ψ
R
{\displaystyle \psi _{L}=\psi _{R}\,\!}
d
d
x
ψ
L
=
d
d
x
ψ
R
−
2
m
λ
ℏ
2
ψ
R
{\displaystyle {\frac {d}{dx}}\psi _{L}={\frac {d}{dx}}\psi _{R}-{\frac {2m\lambda }{\hbar ^{2}}}\psi _{R}\,\!}
特別注意第二個邊界條件方程式,波函數隨位置的導數在
x
=
0
{\displaystyle x=0\,\!}
2
λ
ℏ
2
ψ
R
{\displaystyle {\frac {2\lambda }{\hbar ^{2}}}\psi _{R}\,\!}
x
=
0
{\displaystyle x=0\,\!}
−
ℏ
2
2
m
∫
−
ϵ
ϵ
d
2
ψ
d
x
2
d
x
+
∫
−
ϵ
ϵ
V
(
x
)
ψ
d
x
=
E
∫
−
ϵ
ϵ
ψ
d
x
{\displaystyle -{\frac {\hbar ^{2}}{2m}}\int _{-\epsilon }^{\epsilon }{\frac {d^{2}\psi }{dx^{2}}}\,dx+\int _{-\epsilon }^{\epsilon }V(x)\psi \,dx=E\int _{-\epsilon }^{\epsilon }\psi \,dx\,\!}
(1) 其中,
ϵ
{\displaystyle \epsilon \,\!}
方程式(1)右邊的能量項目是
E
∫
−
ϵ
ϵ
ψ
d
x
≈
E
⋅
2
ϵ
⋅
ψ
(
0
)
{\displaystyle E\int _{-\epsilon }^{\epsilon }\psi \,dx\approx E\cdot 2\epsilon \cdot \psi (0)\,\!}
(2) 當
ϵ
→
0
{\displaystyle \epsilon \to 0\,\!}
方程式(1)左邊是
−
ℏ
2
2
m
(
d
ψ
R
d
x
|
ϵ
−
d
ψ
L
d
x
|
−
ϵ
)
+
λ
∫
−
ϵ
ϵ
δ
(
x
)
ψ
d
x
=
0
{\displaystyle -{\frac {\hbar ^{2}}{2m}}\left({\frac {d\psi _{R}}{dx}}{\bigg |}_{\epsilon }-{\frac {d\psi _{L}}{dx}}{\bigg |}_{-\epsilon }\right)+\lambda \int _{-\epsilon }^{\epsilon }\delta (x)\psi \,dx=0\,\!}
(3) 根據狄拉克Delta函數 的定義,
∫
−
ϵ
ϵ
δ
(
x
)
ψ
d
x
=
ψ
R
(
0
)
{\displaystyle \int _{-\epsilon }^{\epsilon }\delta (x)\psi \,dx=\psi _{R}(0)\,\!}
(4) 而在
ϵ
→
0
{\displaystyle \epsilon \to 0\,\!}
lim
ϵ
→
0
d
ψ
L
d
x
|
−
ϵ
=
d
ψ
L
d
x
|
0
{\displaystyle \lim _{\epsilon \to 0}{\frac {d\psi _{L}}{dx}}{\bigg |}_{-\epsilon }={\frac {d\psi _{L}}{dx}}{\bigg |}_{0}\,\!}
(5)
lim
ϵ
→
0
d
ψ
R
d
x
|
ϵ
=
d
ψ
R
d
x
|
0
{\displaystyle \lim _{\epsilon \to 0}{\frac {d\psi _{R}}{dx}}{\bigg |}_{\epsilon }={\frac {d\psi _{R}}{dx}}{\bigg |}_{0}\,\!}
(6) 將這些結果(4),(5),(6)代入方程式(3),整理後,可以得到第二個邊界條件方程式:在
x
=
0
{\displaystyle x=0\,\!}
d
ψ
L
d
x
=
d
ψ
R
d
x
−
2
m
λ
ℏ
2
ψ
R
{\displaystyle {\frac {d\psi _{L}}{dx}}={\frac {d\psi _{R}}{dx}}-{\frac {2m\lambda }{\hbar ^{2}}}\psi _{R}\,\!}
從這兩個邊界條件方程式。稍加運算,可以得到以下方程式:
A
r
+
A
l
=
B
r
+
B
l
{\displaystyle A_{r}+A_{l}=B_{r}+B_{l}\,\!}
i
k
(
A
r
−
A
l
−
B
r
+
B
l
)
=
2
m
λ
ℏ
2
(
B
r
+
B
l
)
{\displaystyle ik(A_{r}-A_{l}-B_{r}+B_{l})={\frac {2m\lambda }{\hbar ^{2}}}(B_{r}+B_{l})\,\!}
一個Delta位勢阱的反射係數
R
{\displaystyle R\,\!}
T
{\displaystyle T\,\!}
E
{\displaystyle E\,\!}
E
>
0
{\displaystyle E>0\,\!}
λ
2
2
m
ℏ
2
{\displaystyle {\frac {\lambda ^{2}}{2m\hbar ^{2}}}\,\!}
假若,能量是正值的,粒子可以自由的移動於位勢阱外的兩個半空間,
x
<
0
{\displaystyle x<0\,\!}
x
>
0
{\displaystyle x>0\,\!}
散射 行為。稱這粒子的量子態 為散射態 。設定粒子從左邊入射。在Delta位勢阱,粒子可能會被反射回去,或者會被透射過去。我們想要知道散射的反射係數 與透射係數 。設定
A
r
=
1
{\displaystyle A_{r}=1\,\!}
A
l
=
r
{\displaystyle A_{l}=r\,\!}
B
l
=
0
{\displaystyle B_{l}=0\,\!}
B
r
=
t
{\displaystyle B_{r}=t\,\!}
機率幅
r
{\displaystyle r\,\!}
機率幅
t
{\displaystyle t\,\!}
r
=
−
1
i
ℏ
2
k
m
λ
+
1
{\displaystyle r=-\ {\cfrac {1}{{\cfrac {i\hbar ^{2}k}{m\lambda }}+1}}\,\!}
t
=
1
−
i
m
λ
ℏ
2
k
+
1
{\displaystyle t={\cfrac {1}{-\ {\cfrac {im\lambda }{\hbar ^{2}k}}+1}}\,\!}
反射係數是
R
=
|
r
|
2
=
1
1
+
ℏ
4
k
2
m
2
λ
2
=
1
1
+
2
ℏ
2
E
m
λ
2
{\displaystyle R=|r|^{2}={\cfrac {1}{1+{\cfrac {\hbar ^{4}k^{2}}{m^{2}\lambda ^{2}}}}}={\cfrac {1}{1+{\cfrac {2\hbar ^{2}E}{m\lambda ^{2}}}}}\,\!}
這純粹是一個量子力學的效應;在古典力學裏,這是不可能發生的。
透射係數是
T
=
|
t
|
2
=
1
−
R
=
1
1
+
m
2
λ
2
ℏ
4
k
2
=
1
1
+
m
λ
2
2
ℏ
2
E
{\displaystyle T=|t|^{2}=1-R={\cfrac {1}{1+{\cfrac {m^{2}\lambda ^{2}}{\hbar ^{4}k^{2}}}}}={\cfrac {1}{1+{\cfrac {m\lambda ^{2}}{2\hbar ^{2}E}}}}\,\!}
由於模型的對稱性,假若,粒子從右邊入射,我們也會得到同樣的答案。
很奇異地,給予同樣的能量、質量、與狄拉克Delta函數的強度,Delta位勢壘與Delta位勢阱有同樣的反射係數與透射係數。 Delta位勢阱的束縛態,在任何一個位置,波函數都是連續的;可是,除了在
x
=
0
{\displaystyle x=0\,\!}
每一個一維的吸引位勢,都至少會存在著一個束縛態 (bound state )。由於
E
<
0
{\displaystyle E<0\,\!}
κ
=
−
i
k
=
2
m
|
E
|
/
ℏ
2
{\displaystyle \kappa =-ik={\sqrt {2m|E|/\hbar ^{2}}}\,\!}
ψ
L
{\displaystyle \psi _{L}\,\!}
ψ
R
{\displaystyle \psi _{R}\,\!}
x
{\displaystyle x\,\!}
發散 於
x
→
±
∞
{\displaystyle x\to \pm \infty \,\!}
A
r
{\displaystyle A_{r}\,\!}
B
l
{\displaystyle B_{l}\,\!}
ψ
L
(
x
)
=
A
l
e
κ
x
{\displaystyle \psi _{L}(x)=A_{l}e^{\kappa x}\,\!}
ψ
R
(
x
)
=
B
r
e
−
κ
x
{\displaystyle \psi _{R}(x)=B_{r}e^{-\kappa x}\,\!}
從邊界條件與歸一條件 ,可以得到
A
l
=
B
r
=
κ
{\displaystyle A_{l}=B_{r}={\sqrt {\kappa }}\,\!}
κ
=
m
λ
ℏ
2
{\displaystyle \kappa ={\frac {m\lambda }{\hbar ^{2}}}\,\!}
Delta位勢阱只能有一個束縛態。束縛態的能量是
E
=
−
ℏ
2
κ
2
2
m
=
−
m
λ
2
2
ℏ
2
{\displaystyle E=-\ {\frac {\hbar ^{2}\kappa ^{2}}{2m}}=-\ {\frac {m\lambda ^{2}}{2\hbar ^{2}}}\,\!}
束縛態的波函數是
ψ
(
x
)
=
m
λ
ℏ
e
−
m
λ
∣
x
∣
/
ℏ
2
{\displaystyle \psi (x)={\frac {\sqrt {m\lambda }}{\hbar }}e^{-m\lambda \mid x\mid /\hbar ^{2}}\,\!}
Delta位勢阱是有限深方形阱 的一個特別案例。在有限深位勢阱的深度
V
0
→
∞
{\displaystyle V_{0}\to \infty \,\!}
L
→
0
{\displaystyle L\to 0\,\!}
V
0
L
=
λ
{\displaystyle V_{0}L=\lambda \,\!}
當核間距R=2時,雙勢井狄拉克Delta函數模型中的對稱與反對稱的波函數 Delta函數模型其實是氫原子 的一維版本根據維度比例由 達德利·赫施巴赫 (「Dudley R. Herschbach」)[ 1]
雙井迪拉克Delta函數模型是用以下薛丁格方程式描述:
−
ℏ
2
2
m
d
2
ψ
d
x
2
(
x
)
+
V
(
x
)
ψ
(
x
)
=
E
ψ
(
x
)
{\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}(x)+V(x)\psi (x)=E\psi (x)}
電位現為:
V
(
x
)
=
−
q
[
δ
(
x
−
R
2
)
+
λ
δ
(
x
+
R
2
)
]
{\displaystyle V(x)=-q\left[\delta (x-{\frac {R}{2}})+\lambda \delta (x+{\frac {R}{2}})\right]}
其中
0
<
R
<
∞
{\displaystyle 0<R<\infty }
x
=
±
R
2
{\displaystyle x=\pm {\textstyle {\frac {R}{2}}}}
原子單位制 且設
ℏ
=
m
=
1
{\displaystyle \hbar =m=1}
0
<
λ
<
1
{\displaystyle 0<\lambda <1}
擬設 於此解為:
ψ
(
x
)
=
A
e
−
d
|
x
−
R
2
|
+
B
e
−
d
|
x
+
R
2
|
{\displaystyle \psi (x)~=~Ae^{-d\left|x-{\frac {R}{2}}\right|}+Be^{-d\left|x+{\frac {R}{2}}\right|}}
令波函數於Delta函數峰值相等可得行列式 :
|
q
−
d
q
e
−
d
R
q
λ
e
−
d
R
q
λ
−
d
|
=
0
,
E
=
−
d
2
2
.
{\displaystyle \left|{\begin{array}{cc}q-d&qe^{-dR}\\q\lambda e^{-dR}&q\lambda -d\end{array}}\right|=0~,\qquad E=-{\frac {d^{2}}{2}}~.}
因此,
d
{\displaystyle d}
d
±
(
λ
)
=
1
2
q
(
λ
+
1
)
±
1
2
{
q
2
(
1
+
λ
)
2
−
4
λ
q
2
[
1
−
e
−
2
d
±
(
λ
)
R
]
}
1
/
2
{\displaystyle d_{\pm }(\lambda )~=~{\textstyle {\frac {1}{2}}}q(\lambda +1)\pm {\textstyle {\frac {1}{2}}}\left\{q^{2}(1+\lambda )^{2}-4\,\lambda q^{2}\lbrack 1-e^{-2d_{\pm }(\lambda )R}]\right\}^{1/2}}
它有兩解
d
=
d
±
{\displaystyle d=d_{\pm }}
λ
=
1
{\displaystyle \lambda =1}
d
±
=
q
[
1
±
e
−
d
±
R
]
{\displaystyle d_{\pm }=q[1\pm e^{-d_{\pm }R}]}
此「+」代表了對稱於中點的波函數(圖中紅色)而
A
=
B
{\displaystyle A=B}
A
=
−
B
{\displaystyle A=-B}
H
2
+
{\displaystyle H_{2}^{+}}
[ 2]
d
±
=
q
+
W
(
±
q
R
e
−
q
R
)
/
R
{\displaystyle d_{\pm }=q~+~W(\pm qRe^{-qR})/R}
其中W是標準朗伯W函數 注意此最低能對應於對稱解
d
+
{\displaystyle d_{+}}
朗伯W函數 章節與相關參考)。
^ D.R Herschbach , J.S. Avery, and O. Goscinski (eds.), Dimensional Scaling in Chemical Physics , Springer, (1992). [1] (頁面存檔備份 ,存於網際網路檔案館 )^ T.C. Scott, J.F. Babb, Alexander Dalgarno and John D. Morgan III, "The Calculation of Exchange Forces: General Results and Specific Models", J. Chem. Phys. , 99, pp. 2841-2854, (1993). [2]





































































![{\displaystyle V(x)=-q\left[\delta (x-{\frac {R}{2}})+\lambda \delta (x+{\frac {R}{2}})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9938cb4c9100459ff028312655ff7f02be1d67f)







![{\displaystyle d_{\pm }(\lambda )~=~{\textstyle {\frac {1}{2}}}q(\lambda +1)\pm {\textstyle {\frac {1}{2}}}\left\{q^{2}(1+\lambda )^{2}-4\,\lambda q^{2}\lbrack 1-e^{-2d_{\pm }(\lambda )R}]\right\}^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02509c77fbbd368bfbb4680bfed7062d06a7eedc)


![{\displaystyle d_{\pm }=q[1\pm e^{-d_{\pm }R}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de3c25340e952fe2d73d65c9047a1eab7295c663)




