截半正一百二十胞體
外觀
| 截半正一百二十胞體 | |
|---|---|
 | |
| 類型 | 均勻多胞體 |
| 數學表示法 | |
| 考克斯特符號 | |
| 施萊夫利符號 | t1{5,3,3} |
| 性質 | |
| 胞 | 720 包括: 120(3.5.3.5) 600(3.3.3) |
| 面 | 3120 包括: 2400 {3}, 720 {5} |
| 邊 | 3600 |
| 頂點 | 1200 |
| 組成與佈局 | |
| 頂點圖 | 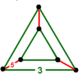 三角柱 |
| 對稱性 | |
| 考克斯特群 | H4 or [3,3,5] |
| 特性 | |
| convex, 邊可遞 | |
在幾何學里,截半正一百二十胞體是一個由600個正四面體和120個截半二十面體胞構成的均勻多胞體。其頂點圖是一個三角柱,每個頂點周圍有3個截半二十面體和2個正四面體。
投影
[編輯]| 三維正射投影 | |
|---|---|

|
截半正一百二十胞體的三維正射投影,對著一個截半二十面體胞。 |
| H4 | - | F4 |
|---|---|---|
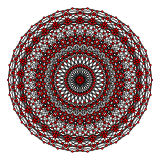 [30] |
 [20] |
 [12] |
| H3 | A2 / B3 / D4 | A3 / B2 |
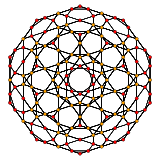 [10] |
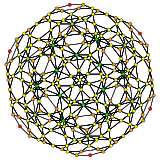 [6] |
 [4] |
參考文獻
[編輯]- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] (頁面存檔備份,存於網際網路檔案館)
- (Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Four-dimensional Archimedian Polytopes (頁面存檔備份,存於網際網路檔案館) (German), Marco Möller, 2004 PhD dissertation [2] (頁面存檔備份,存於網際網路檔案館)
外部連結
[編輯]- Convex uniform polychora based on the hecatonicosachoron (120-cell) and hexacosichoron (600-cell) - Model 33, George Olshevsky.
- rectified 120-cell (頁面存檔備份,存於網際網路檔案館) Marco Möller's Archimedean polytopes in R4 (German)
- Klitzing, Richard. 4D uniform polytopes (polychora) o3o3x5o - rahi. bendwavy.org.
