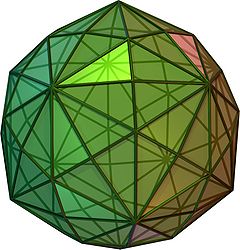
四角化菱形三十面体
 (按这里观看旋转模型) | ||||
| 类别 | 卡塔兰立体 一百二十面体 | |||
|---|---|---|---|---|
| 对偶多面体 | 大斜方截半二十面体 | |||
| 识别 | ||||
| 鲍尔斯缩写 | siddykat | |||
| 数学表示法 | ||||
| 考克斯特符号 | ||||
| 康威表示法 | mD 或 dbD | |||
| 性质 | ||||
| 面 | 120 | |||
| 边 | 180 | |||
| 顶点 | 62 | |||
| 欧拉特征数 | F=120, E=180, V=62 (χ=2) | |||
| 二面角 | 164° 53′ 17′′ arccos(-179-24√5/241) | |||
| 组成与布局 | ||||
| 面的种类 |  不等边三角形 | |||
| 面的布局 | V4.6.10 | |||
| 顶点的种类 | 20个6阶顶点 30个4阶顶点 12个10阶顶点 | |||
| 对称性 | ||||
| 对称群 | Ih, H3, [5,3], (*532) | |||
| 旋转对称群 | I, [5,3]+, (532) | |||
| 图像 | ||||
| ||||
在几何学中,四角化菱形三十面体又称为角锥化菱形三十面体(kisrhombic triacontahedron[1]:284)或六角化二十面体(hexakis icosahedron[2]:55)是具有120个面的卡塔兰立体,并且是阿基米德立体——大斜方截半二十面体的对偶多面体[3][4]。这种立体是一个等面图形,也就是说它每个面都全等,但组成面不是正多边形,严格来说是不等边三角形。其外观有点像膨胀的菱形三十面体:若将菱形三十面体的每个菱形面替换成1个顶点和4个三角形面则会形成四角化菱形三十面体,也可以视为在菱形三十面体的每个面上叠上菱形四角锥来构成,也就是说,四角化菱形三十面体是菱形三十面体的克利多面体。四角化菱形三十面体是阿基米德立体和卡塔兰立体中面数最多的立体,面数最多的阿基米德立体是扭棱十二面体有92个面。
如果排除双锥体、双锥反柱体和偏方面体,则在任何其他严格凸多面体中,四角化菱形三十面体是每个面都具有相同的形状的立体中,面数最多的多面体。
若将四角化菱形三十面体投影到球面上,则四角化菱形三十面体定义了15个大圆。巴克敏斯特·富勒使用这15个大圆,以及另外两个多面体中的10个大圆和6个大圆来定义球面二十面体的31个大圆。
性质
[编辑]四角化菱形三十面体共有120个面、180个边和62个顶点[5]。在其120个面中,每个面都是全等的不等边三角形。在其62个顶点中,有20个顶点是6个三角形的公共顶点、30个顶点是4个三角形的公共顶点和12个顶点是10个三角形的公共顶点[6]。
面的组成
[编辑]组成四角化菱形三十面体的面为不等边三角形。其三个内角分别为、 和[7],其中为黄金比例。
其中有一个角非常接近直角,但不是直角,因此这个三角形不是直角三角形。其三个边的边长比(由短到长)为:[6]
- 1.3942870166557737040 : 2.19017447980650378252 : 2.5755459331956214849
也就是说,若最短边长为单位长,则另外两边长分别为1.57082039324994[8][6]和1.84721359549996[9][6]。这三种边长的边在整个立体中各有60条。[6]
二面角
[编辑]四角化菱形三十面体只有一种二面角,约为164.888度:[6]
- 2.87783661046122428164.887891908°
顶点坐标
[编辑]四角化菱形三十面体的62个顶点分别落在以下3个集合内:[6]
- 其中12个顶点的形式为的循环排列,其中为黄金比例。这些顶点之间形成一个正二十面体。
- 其中20个顶点的形式为或的循环排列,其中为黄金比例。这些顶点之间形成一个正十二面体。
- 剩下的30个顶点为上述32个顶点所构成的菱形三十面体之面心经一个倍率1.065091570621743缩放后的顶点,其中为黄金比例。上述32个顶点之间会构成一个菱形三十面体,这个菱形三十面体的30个面的面心为和的循环排列,经由倍率缩放后变为和的循环排列,共30个顶点,这30个顶点为四角化菱形三十面体的最后30个顶点。
用途
[编辑]由于四角化菱形三十面体是等面的120面体,因此可以以此形状制作120面的骰子。[10]通常使用3D打印来制作这种形状的骰子[11]。自2016年以来,Dice Lab已使用四角化菱形三十面体的模具注塑成型来大规模销售120面的骰子。[12]据称120面骰是公正骰子最大的可能面数,虽然可以用无限集合的等面立体(如双锥体、双锥反柱体或偏方面体)来制作更多面数的骰子,但由于这种形状(更多面的双锥体、双锥反柱体或偏方面体)会导致制成的骰子长时间滚动,因此在现实中并不实用。[13]
作为正十二面体的四角化菱形三十面体,即把正十二面体的每个五边形面分割成10个三角形的这种形状可以设计成一种魔术方块,通常称为Big Chop。然而如何至制作出这种形状的魔术方块目前仍是未解决的问题,目前还没有令人满意的设计结构。[14]
Brilliant的标志是投影到球面上的四角化菱形三十面体,Brilliant是一个包含理工科相关主题的系列课程的网站。[15]此外由于其等面的特性,加上面数非常多,因此曾被用来建构全球离散格网[16]。
-
120面的骰子
-
Big Chop魔方
参见
[编辑]参考文献
[编辑]- ^ Conway, J.H. and Burgiel, H. and Goodman-Strauss, C. The Symmetries of Things. AK Peters/CRC Recreational Mathematics Series. CRC Press. 2016 [2022-07-23]. ISBN 9781439864890. LCCN 2007046446. (原始内容存档于2022-07-26).
- ^ Alan Holden. Shapes, Space, and Symmetry. New York: Columbia University Press. 1971.
- ^ Weisstein, Eric W. (编). Disdyakis Triacontahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Robert Webb. Disdyakistriacontahedron. software3d.com. [2022-07-24]. (原始内容存档于2021-03-02).
- ^ V. Bulatov. disdyakistriacontahedron. bulatov.org. 2009 [2022-07-24]. (原始内容存档于2021-10-30).
- ^ 6.0 6.1 6.2 6.3 6.4 6.5 6.6 David I. McCooey. Catalan Solids: Disdyakis Triacontahedron. [2022-07-23]. (原始内容存档于2022-02-14).
- ^ Disdyakis triacontahedron. fillygons.ch. [2022-07-23]. (原始内容存档于2022-07-26).
- ^ Wolfram, Stephen. "(3*sqrt(15*(65+19*sqrt(5)))/55)/(sqrt(15*(85−31*sqrt(5)))/11)". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ Wolfram, Stephen. "(2*sqrt(15*(5−sqrt(5)))/5)/(sqrt(15*(85−31*sqrt(5)))/11)". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ The Mind-Boggling Challenge of Designing 120-Sided Dice. wired.com. [2022-07-23]. (原始内容存档于2022-08-11).
- ^ Kevin Cook's Dice Collector website: d120 3D printed from Shapeways artist SirisC. dicecollector.com. [2022-07-24]. (原始内容存档于2022-04-10).
- ^ d120 and d48. The Dice Lab. (原始内容存档于2016-12-08).
- ^ This D120 is the Largest Mathematically Fair Die Possible | Nerdist. (原始内容存档于2016-05-03).
- ^ Big Chop. twistypuzzles.com. [2022-07-24]. (原始内容存档于2022-07-30).
- ^ Brilliant | Learn to think. brilliant.org. [2020-02-01]. (原始内容存档于2022-08-22) (美国英语).
- ^ Hall, John and Wecker, Lakin and Ulmer, Benjamin and Samavati, Faramarz. Disdyakis triacontahedron DGGS. ISPRS International Journal of Geo-Information (MDPI). 2020, 9 (5): 315 [2022-07-24]. (原始内容存档于2022-07-26).