精确覆盖问题

在一个全集X中若干子集的集合为S，精确覆盖是指，S的子集S*，满足X中的每一个元素在S*中恰好出现一次。

在计算机科学中，精确覆盖问题指找出这样的一种覆盖，或证明其不存在。这是一个NP-完全问题，也是卡普的二十一个NP-完全问题之一。

定义

满足以下条件的集合为一个精确覆盖：

• S*中任意两个集合没有交集，即X中的元素在S*中出现最多一次
• S*中集合的全集为X，即X中的元素在S*中出现最少一次

合二为一，即X中的元素在S*中出现恰好一次。

举例

令 ${\mathcal {S}}$ = {N, O, E, P} 是集合X = {1, 2, 3, 4}的一个子集的集合，并满足：

• N = { }
• O = {1, 3}
• E = {2, 4}
• P = {2, 3}.

其中一个子集 {O, E} 是 X的一个精确覆盖,因为 O = {1, 3} 而 E = {2, 4} 的并集恰好是 X = {1, 2, 3, 4}。同理， {N, O, E} 也是 X.的一个精确覆盖。空集并不影响结论。

关系表示

通常我们用S的每个子集与X的元素之间包含关系的二元关系来表示精确覆盖问题。

矩阵表示法

包含关系可以用一个关系矩阵表示。. 矩阵每行表示S的一个子集，每列表示X中的一个元素。矩阵行列交点元素为1表示对应的元素在对应的集合中，不在则为0.

通过这种矩阵表示法，求一个精确覆盖转化为求矩阵的若干个行的集合，使每列有且仅有一个1。同时，该问题也是精确覆盖的典型例题之一。

下图为其中一个例子：

	1	2	3	4	5	6	7
A	1	0	0	1	0	0	1
B	1	0	0	1	0	0	0
C	0	0	0	1	1	0	1
D	0	0	1	0	1	1	0
E	0	1	1	0	0	1	1
F	0	1	0	0	0	0	1

S* = {B, D, F} 便是一个精确覆盖。

图论表示法

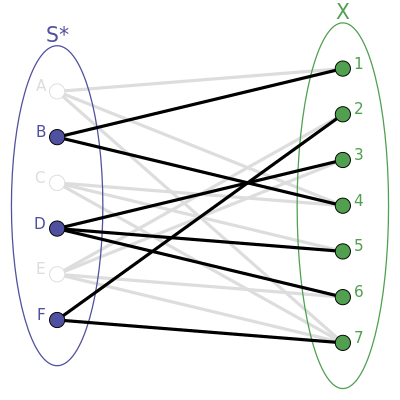
包含关系也可以用一个二分图表示。

二分图左侧每个节点表示S的每个集合，右侧每个节点表示X的每个元素，而精确覆盖便是一种匹配，满足右侧的每个点恰好有一条边。

求解方法

X算法是高德纳提出的解决该问题的算法，而舞蹈链算法(Dancing Links，DLX)算法是X算法在计算机上的一种高效实现。

应用举例

• 数独求解