大菱形三十面体

大菱形三十面体

类别	均匀多面体对偶 星形多面体 星形菱形三十面体
对偶多面体	大截半二十面体
识别
名称	大菱形三十面体
参考索引	DU54
数学表示法
考克斯特符号
性质
面	30
边	60
顶点	32
欧拉特征数	F=30, E=60, V=32 （χ=2）
亏格	0
二面角	72度
组成与布局
面的种类	菱形
顶点布局	两种顶点 10个菱形的公共顶点 6个菱形的公共顶点
对称性
对称群	Ih, [5,3], *532
特性
等面、等边、非凸
图像
大截半二十面体 （对偶多面体）

在几何学中，大菱形三十面体是一种非凸的等面等边三十面体，其对偶多面体为大截半二十面体。

性质

大菱形三十面体共有30个面、60条边和32个顶点，其32个面都是全等的菱形。

其每个菱形上与其他面之交线的位置也都相等。每个菱形只有四个角的部分露出，其他部分阶隐没在立体图形内部，露出的部分为4个凹六边形，在上图以蓝色表示。

大菱形三十面体共有2种顶角，其顶点图分别为五角星和三角形。顶点图为五角星的顶角是菱形的钝角，为5个菱形的公共顶点；顶点图为三角形的顶角是菱形的锐角，为3个菱形的公共顶点。

大菱形三十面体可以通过将菱形三十面体的菱形面放大黄金比例的三次方倍，也就是$\varphi ^{3}=1+2\varphi \!$倍大来构造。大菱形三十面体的星状核为菱形三十面体，因此其也是一种星形菱形三十面体。

顶点座标

对偶边长为1大菱形三十面体的顶点座标为：

$(0,\pm {\frac {5-{\sqrt {5}}}{8}},\pm {\frac {3{\sqrt {5}}-5}{8}})$

$(\pm {\frac {5-{\sqrt {5}}}{8}},\pm {\frac {3{\sqrt {5}}-5}{8}},0)$

$(\pm {\frac {3{\sqrt {5}}-5}{8}},0,\pm {\frac {5-{\sqrt {5}}}{8}})$

$(\pm {\frac {\sqrt {5}}{4}},0,\pm {\frac {3{\sqrt {5}}-5}{8}})$

$(0,\pm {\frac {3{\sqrt {5}}-5}{8}},\pm {\frac {\sqrt {5}}{4}})$

$(\pm {\frac {3{\sqrt {5}}-5}{8}},\pm {\frac {\sqrt {5}}{4}},0)$

$(\pm {\frac {5-{\sqrt {5}}}{8}},\pm {\frac {5-{\sqrt {5}}}{8}},\pm {\frac {5-{\sqrt {5}}}{8}})$

作为星形多面体

内侧菱形三十面体可以看作是一种菱形三十面体的星形多面体，即星形菱形三十面体。

星状图	星形	星状核	凸包
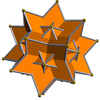
		菱形三十面体	正十二面体

对偶多面体

主条目：大截半二十面体

大菱形三十面体的对偶多面体是大截半二十面体，其在非凸均匀多面体被编号为U₅₄。其在施莱夫利符号中可以用r{3,5/2}表示，其为大星形十二面体和大二十面体的截半多面体。

使用

大菱形三十面体被考克斯特认为是一种具代表性的星形多面体，且被放在其写的书籍《正多胞形》的封面上。此外，有一些魔术方块外型被制作成大菱形三十面体的形状。

相关多面体

对偶复合体

大菱形三十面体与其对偶的复合体为复合大截半二十面体大菱形三十面体。其共有62个面、120条边和62个顶点，其尤拉示性数为4，亏格为-1，具有12个非凸面，在威佐夫记号中以(2 | ⁵/₂ 3)表示。

参考文献

1. Wenninger, Magnus. Polyhedron Models. Cambridge University Press. 1974. ISBN 0-521-09859-9. 
2. Wenninger, Magnus. Dual Models. Cambridge University Press. 1983. ISBN 0-521-54325-8. 
3. Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F. The fifty-nine icosahedra 3rd. Tarquin. 1999. ISBN 978-1-899618-32-3. MR676126.  (1st Edn University of Toronto (1938))

外部链接

• 埃里克·韦斯坦因. 大菱形三十面體. MathWorld.