以法國數學家米歇爾·羅爾命名的羅爾中值定理(英語:Rolle's theorem)是微分學中一條重要的定理,是三大微分中值定理之一,敘述如下:如果函數 滿足
滿足
- 在閉區間
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 上連續;
上連續;
- 在開區間
 內可微分;
內可微分;
- 在區間端點處的函數值相等,即
 ,
,
那麼在 內至少有一點
內至少有一點 ,使得
,使得 [1]。
[1]。
 羅爾定理的幾何意義
羅爾定理的幾何意義
首先,因為 在閉區間
在閉區間![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 上連續,根據極值定理,
上連續,根據極值定理, 在
在![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 上有最大值和最小值。如果最大值和最小值都在端點
上有最大值和最小值。如果最大值和最小值都在端點 或
或 處取得,由於
處取得,由於 ,
, 顯然是一個常數函數。那麼對於任一點
顯然是一個常數函數。那麼對於任一點 ,我們都有
,我們都有 。
。
現在假設 在
在 處取得最大值。我們只需證明
處取得最大值。我們只需證明 在該點導數為零。
在該點導數為零。
取 ,由最大值定義
,由最大值定義 ,那麼
,那麼 。令
。令 ,則
,則 。因為
。因為 在
在 處可導,所以我們有
處可導,所以我們有 。
。
取 ,那麼
,那麼 。這時令
。這時令 ,則有
,則有 ,所以
,所以 。
。
於是,結合兩者, 。
。
 在
在 處取得最小值的情況同理。
處取得最小值的情況同理。
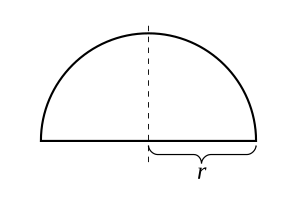 半徑為r的半圓
半徑為r的半圓
考慮函數
![{\displaystyle f(x)={\sqrt {r^{2}-x^{2}}},\quad x\in [-r,r]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/391b511e2cdd527afa0af72594961152b5c616d7) 。
。
(其中r > 0。)它的圖像是中心位於原點的半圓。這個函數在閉區間[−r,r]內連續,在開區間(−r,r)內可導(但在終點−r和r處不可導)。由於f(−r) = f(r),因此根據羅爾定理,存在一個導數為零的點。
 絕對值函數的圖像
絕對值函數的圖像
如果函數在區間內的某個點不可導,則羅爾定理的結論不一定成立。對於某個a > 0,考慮絕對值函數:
![{\displaystyle f(x)=|x|,\qquad x\in [-a,a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fafefd1cec41258d1e6aaa96a40d4860be8a1672) 。
。
那麼f(−a) = f(a),但−a和a之間不存在導數為零的點。這是因為,函數雖然是連續的,但它在點x = 0不可導。注意f的導數在x = 0從-1變為1,但不取得值0。
第二個例子表明羅爾定理下面的一般形式:
考慮一個實數,f(x)是在閉區間[a,b]上的連續函數,並滿足f(a) = f(b).如果對開區間(a,b)內的任意x,右極限

而左極限

在擴展的實數軸[−∞,∞]上存在,那麼開區間(a,b)內就存在c使得這兩個極限
 和
和
中其中一個≥ 0,另一個≤ 0(在擴展的實數軸上)。如果對任何x左極限和右極限都相同,那麼它們對c也相等,於是在c處f的導函數存在且等於零。






![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)





















![{\displaystyle f(x)={\sqrt {r^{2}-x^{2}}},\quad x\in [-r,r]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/391b511e2cdd527afa0af72594961152b5c616d7)
![{\displaystyle f(x)=|x|,\qquad x\in [-a,a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fafefd1cec41258d1e6aaa96a40d4860be8a1672)



