交替截角八面體堆砌
外觀
| 交替截角八面體堆砌 | |
|---|---|
 | |
| 類型 | 均勻堆砌 |
| 維度 | 3 |
| 數學表示法 | |
| 考克斯特符號 | |
| 考克斯特記號 | [4[3[4]]] ↔ [[4,3,4]] |
| 纖維流形記號 | 8o:2 |
| 施萊夫利符號 | 2s{4,3,4} |
| 性質 | |
| 胞 | (3.3.3.3.3) (3.3.3) |
| 面 | {3} {3} |
| 組成與佈局 | |
| 頂點圖 |  |
| 對稱性 | |
| 對稱群 | , [4,3,4] |
| 空間群 | Im3m (229) |
| 考克斯特群 | [4,3,4], |
| 特性 | |
| 頂點正 | |
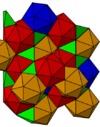
在幾何學中,交替截角八面體堆砌或交錯截角八面體堆砌又稱為雙扭稜立方體堆砌[1]是三維空間內28個半正密鋪之一,由截角八面體堆砌交替截去截角八面體胞的頂點產生擬正二十面體,剩餘空隙使用楔形四面體填滿而成。
交替截角八面體堆砌有三個相關的考克斯特圖結構:![]()
![]()
![]()
![]()
![]()
![]()
![]() 、
、![]()
![]()
![]()
![]()
![]() 和
和![]()
![]()
![]()
![]()
![]() ,他們分別存在[4,3+,4]、[4,(31,1)+]與[3[4]]+的對稱性,第一個[[4,3+,4]]和最後一個[[3[4]]]+的對稱性可以增加一倍。
,他們分別存在[4,3+,4]、[4,(31,1)+]與[3[4]]+的對稱性,第一個[[4,3+,4]]和最後一個[[3[4]]]+的對稱性可以增加一倍。
表面塗色
[編輯]交替截角八面體堆砌有五種不同的表面塗色,其佈局與截角八面體堆砌的五種表面塗色相似。下表列出各表面塗色的性質:
| 空間群 | I3 (204) | Pm3 (200) | Fm3 (202) | Fd3 (203) | F23 (196) |
|---|---|---|---|---|---|
| 纖維流形 | 8−o | 4− | 2− | 2o+ | 1o |
| 考克斯特群 | [[4,3+,4]] | [4,3+,4] | [4,(31,1)+] | [[3[4]]]+ | [3[4]]+ |
| 考克斯特符號 | |||||
| 階 | 二 | 全 | 半 | 四分之一 二 |
四分之一 |
| 圖像 表面依胞 上色 |

|

|
|

|

|
自然界中的交替截角八面體堆砌
[編輯]交替截角八面體堆砌是一些分子的晶體結構,例如:α-菱形面體晶系,屬於此種晶體結構的有α-菱形硼[2],交替截角八面體堆砌可以代表其中的硼原子。
交替截角八面體也可以表示面心立方晶格。二十面體的中心位於面心立方晶格的位置。[3]
參考文獻
[編輯]- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (包含11個凸半正鑲嵌、28個凸半正堆砌、和143個凸半正四維砌的全表)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication參與編輯, 1995, ISBN 978-0-471-01003-6 [1](頁面存檔備份,存於互聯網檔案館)
- (22頁) H.S.M.考克斯特, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 半正空間鑲嵌)
- A. Andreini, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
- ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)
- ^ Nelmes et al. 1993.
- ^ Williams, 1979, p 199, Figure 5-38.


