 奧古斯丁·菲涅耳
奧古斯丁·菲涅耳
 古斯塔夫·基爾霍夫
古斯塔夫·基爾霍夫
在光學裏,菲涅耳-基爾霍夫繞射公式(Fresnel-Kirchoff's diffraction formula)可以應用於光波傳播的理論分析模型或數值分析模型。[1][2]從菲涅耳-基爾霍夫繞射公式,可以推導出惠更斯-菲涅耳原理,並且解釋一些惠更斯-菲涅耳原理無法解釋的物理現象與結果。菲涅耳-基爾霍夫繞射公式常被稱為「基爾霍夫繞射公式」(Kirchoff's diffraction formula)。
從基爾霍夫積分定理,在假定一些近似之後,可以推導出菲涅耳-基爾霍夫繞射公式。
惠更斯原理是克里斯蒂安·惠更斯於1678年提出的關於波傳播的理論。惠更斯原理表明,假設在時間 由主波源Q0發射出的球面波,在時間
由主波源Q0發射出的球面波,在時間 傳播到波前
傳播到波前 ,那麼位於波前
,那麼位於波前 的每一個面元素向量
的每一個面元素向量 都可以被視為一個次波源,所有從這些次波源發射出的次波,在之後時間
都可以被視為一個次波源,所有從這些次波源發射出的次波,在之後時間 波前的包絡面就是主波源Q0所發射出的球面波在時間
波前的包絡面就是主波源Q0所發射出的球面波在時間 的波前。
的波前。
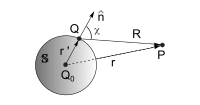 從主波源Q0發射出的球面波,其波前
從主波源Q0發射出的球面波,其波前 的每一點Q都可以視為次波源,它們會發射出次波,在空間任意一點P的波擾是所有這些次波在該點P的相干疊加。
的每一點Q都可以視為次波源,它們會發射出次波,在空間任意一點P的波擾是所有這些次波在該點P的相干疊加。
波動有兩個基本屬性:
惠更斯原理只闡述了前一條屬性,奧古斯丁·菲涅耳將惠更斯提出的次波的概念加以延伸,提出用「次波相干疊加」的點子來解釋繞射現象,這就是惠更斯-菲涅耳原理。這原理表明,波前 的每個面元素向量
的每個面元素向量 都可以視為次波源,它們會發射出次波,在空間任意一點P的波擾是所有這些次波在該點P的相干疊加。設定位於波前
都可以視為次波源,它們會發射出次波,在空間任意一點P的波擾是所有這些次波在該點P的相干疊加。設定位於波前 的任意一點Q,它在點P貢獻的複振幅為
的任意一點Q,它在點P貢獻的複振幅為 ;其中,
;其中, 、
、 分別為點P、點Q的位置。在點P的總波擾為
分別為點P、點Q的位置。在點P的總波擾為
 。
。
為了將這公式具體化,菲涅耳憑藉直覺對 作出了如下假設:
作出了如下假設:
 。
。
 。
。
- 次波源發射出的次波應是球面波,其中
 是波數:
是波數:
 ;其中,
;其中, 是從點Q到點P的位移向量。
是從點Q到點P的位移向量。
- 次波源發射出的次波是各向異性的。假設
 是與面元素向量
是與面元素向量 同方向的單位向量,
同方向的單位向量, 是
是 與
與 之間的夾角,則傾斜因子
之間的夾角,則傾斜因子 與
與 的關係為
的關係為
 。
。
根據以上假設可以得到如下菲涅耳繞射積分公式
 ;
;
其中, 是比例常數。
是比例常數。
在菲涅耳繞射積分公式提出六十餘年後,古斯塔夫·基爾霍夫用嚴格的數學理論推導出菲涅耳-基爾霍夫繞射公式:[3]
![{\displaystyle \psi (\mathbf {r} )=-\ {\frac {i\psi _{0}}{2\lambda }}\oint _{\mathbb {S} }\left({\frac {e^{ik(r'+R)}}{r'R}}\right)[\cos \alpha +\cos \chi ]\,\mathrm {d} S'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95056bcf907df65cfb6994bcc5f3863cc3cf4729) ;
;
其中, 、
、 分別是
分別是 、
、 與
與 之間的夾角。
之間的夾角。
推論從點光源Q0發射的單色光波,其波擾的數值大小與傳播距離成反比,在位置 以方程式表達為
以方程式表達為 。又在其發射出的球面波的波前任意位置,
。又在其發射出的球面波的波前任意位置, 與
與 同向,夾角
同向,夾角 。設定比例常數
。設定比例常數 ,
,
 ,則可得到菲涅耳繞射積分公式。
,則可得到菲涅耳繞射積分公式。
 點P在閉合曲面
點P在閉合曲面 之外。位於點P的波擾
之外。位於點P的波擾 ,可以以位於閉合曲面
,可以以位於閉合曲面 的所有波擾與其梯度表達。
的所有波擾與其梯度表達。
基爾霍夫積分定理應用格林第二恆等式來推導出齊次波動方程式的解答,這解答是以波動方程式在任意閉合曲面 的每一個點的解答和其一階導數來表達。[4]
的每一個點的解答和其一階導數來表達。[4]
對於單頻率波,解答為
![{\displaystyle \psi (\mathbf {r} )={\frac {1}{4\pi }}\oint _{\mathbb {S} }\left[\psi (\mathbf {r} ')\nabla '\left({\frac {e^{ikR}}{R}}\right)-\left({\frac {e^{ikR}}{R}}\right)\nabla '\psi (\mathbf {r} ')\right]\cdot \,\mathrm {d} \mathbf {S} '}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8aa86dc8360be9cab45faab661ea3f9c06922c8) ,
,
或者
![{\displaystyle \psi (\mathbf {r} )={\frac {1}{4\pi }}\oint _{\mathbb {S} }\left[\psi (\mathbf {r} '){\frac {\partial }{\partial n'}}\left({\frac {e^{ikR}}{R}}\right)-\left({\frac {e^{ikR}}{R}}\right){\frac {\partial \psi (\mathbf {r} ')}{\partial n'}}\right]\,\mathrm {d} S'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e96278c09f0fd019ee85b12fa33b7392584ca84c) ;
;
其中, 、
、 分別是從點Q0到點P、點Q的位移向量,
分別是從點Q0到點P、點Q的位移向量, 是在點P的波擾,
是在點P的波擾, 是從點Q到點P的位移向量,
是從點Q到點P的位移向量, 是其數值大小,
是其數值大小, 是波數,
是波數, 是對於源位置
是對於源位置 的梯度,
的梯度, 是從閉合曲面
是從閉合曲面 向外指出的微小面元素向量,
向外指出的微小面元素向量, 是閉合曲面
是閉合曲面 的法向導數。
的法向導數。
在推導基爾霍夫繞射公式的過程中,基爾霍夫做了以下假定:
- 點波源與孔隙之間的距離
 超大於波長
超大於波長 。
。
 超大於波長
超大於波長 。
。
從點波源Q0發射的單頻率波,其能量與傳播距離平方成反比,波擾的數值大小與傳播距離成反比,在點Q的波擾以方程式表達為
 ;
;
其中, 是複值波幅。
是複值波幅。
假設點P在閉合曲面 之外,應用基爾霍夫積分定理的方程式,可以得到在點P的波擾:
之外,應用基爾霍夫積分定理的方程式,可以得到在點P的波擾:
![{\displaystyle \psi (\mathbf {r} )={\frac {\psi _{0}}{4\pi }}\oint _{\mathbb {S} }\left[\left({\frac {e^{ikr'}}{r'}}\right)\nabla '\left({\frac {e^{ikR}}{R}}\right)-\left({\frac {e^{ikR}}{R}}\right)\nabla '\left({\frac {e^{ikr'}}{r'}}\right)\right]\cdot \,{\hat {\mathbf {n} }}\mathrm {d} S'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c759f4cb7ee95e5784775a7bbdfa5f519e4cf08) ;
;
其中, 是與
是與 同方向的單位向量。
同方向的單位向量。
注意到球面出射波的梯度為
 、
、 。
。
從基爾霍夫所做的假定, 、
、 (例如,假設距離大約為1mm,則對於波長在0.4μm至0.7μm之間的可見光,可以做這假定;但對於波長在1mm至1m之間的微波,這假定不適用),則上述兩個公式近似為
(例如,假設距離大約為1mm,則對於波長在0.4μm至0.7μm之間的可見光,可以做這假定;但對於波長在1mm至1m之間的微波,這假定不適用),則上述兩個公式近似為
 、
、
 。
。
所以,在點P的波擾
 ;
;
其中, 、
、 分別是
分別是 、
、 與
與 之間的夾角。
之間的夾角。
這就是菲涅耳-基爾霍夫繞射公式,或基爾霍夫繞射公式。[3]
 傾斜因子
傾斜因子 為
為![{\displaystyle [1+\cos(\chi )]/2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/295b98404bec9961d59e831cf2dcb29630143ad3) 。
。
如右圖所示,假設閉合曲面 是圓球面,點波源Q0與圓球面
是圓球面,點波源Q0與圓球面 的圓心同點。在圓球面
的圓心同點。在圓球面 的任意位置,
的任意位置, 與
與 同向,所以,
同向,所以,
 。
。
注意到 是圓球面
是圓球面 的半徑,對於這積分,
的半徑,對於這積分, 值不變,可以從積分裏提出。在點P的波擾為
值不變,可以從積分裏提出。在點P的波擾為
 ;
;
其中, 為傾斜因子。
為傾斜因子。
應用惠更斯-菲涅耳原理,所得到在點P的波擾的方程式,就是這方程式。但是,惠更斯-菲涅耳原理無法解釋相位差與傾斜因子的物理原因。傾斜因子使得次波的波幅會因為傳播方向而不同;朝着主波方向,波幅較大;逆着主波方向,波幅較小。這解釋了為甚麼波動只會朝着前方傳播的物理現象。[3]
仔細詮釋惠更斯-菲涅耳原理的方程式:從點波源Q0發射的波幅為 的球面波,在點Q的波擾為
的球面波,在點Q的波擾為 ;而從點Q發射的次波,將傾斜因子與相位差納入考量,所貢獻出的波擾,在點P為
;而從點Q發射的次波,將傾斜因子與相位差納入考量,所貢獻出的波擾,在點P為
 。
。
總合所有與點Q同波前的點次波源在點P所貢獻出的波擾,就可以得到 。
。
換另一種直接方法來詮釋,從點波源Q0發射的球面波,在點P的波擾為
 。
。
假若這兩種詮釋都正確,則從這兩種 的表達式分別計算出的結果,應該可以被核對為相等:
的表達式分別計算出的結果,應該可以被核對為相等:
 。
。
為了簡易計算,假設 ,則以下近似成立:
,則以下近似成立:
 、
、 、
、 ;
;
其中, 為
為 與
與 之間的夾角。
之間的夾角。
所以,在點P的波擾可以近似為
![{\displaystyle {\begin{aligned}\psi (\mathbf {r} )&\approx -\ {\frac {i\psi _{0}}{2\lambda }}{\frac {e^{ik(r'+r)}}{r'r}}\int _{0}^{\pi }e^{-ikr'\cos(\theta )}[1+\cos(\theta )]2\pi r'^{2}\sin(\theta )\mathrm {d} \theta \\&\approx -\ {\frac {ik\psi _{0}r'e^{ik(r'+r)}}{2r}}\int _{0}^{\pi }e^{-ikr'\cos(\theta )}[1+\cos(\theta )]\sin(\theta )\mathrm {d} \theta \\&\approx -\ {\frac {ik\psi _{0}r'e^{ik(r'+r)}}{2r}}\ {\frac {2[\sin(kr')+i\cos(kr')]}{kr'}}\\&\approx \psi _{0}{\frac {e^{ikr}}{r}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcdbc9c562b92d47605d3873eb91626446079b18) 。
。
假設波源為有限尺寸,位於曲面 的波擾表達為
的波擾表達為 ,則位於點P的波擾為
,則位於點P的波擾為
![{\displaystyle \psi (\mathbf {r} )={\frac {1}{4\pi }}\oint _{\mathbb {S} }\left[\psi (\mathbf {r} '){\frac {\partial }{\partial n'}}\left({\frac {e^{ikR}}{R}}\right)-\left({\frac {e^{ikR}}{R}}\right){\frac {\partial \psi (\mathbf {r} ')}{\partial n'}}\right]\,\mathrm {d} S'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e96278c09f0fd019ee85b12fa33b7392584ca84c) 。
。
假定 ,則
,則
![{\displaystyle \psi (\mathbf {r} )=-\ {\frac {1}{4\pi }}\oint _{\mathbb {S} }\left({\frac {e^{ikR}}{R}}\right)\left[ik\psi (\mathbf {r} ')\cos {({\hat {\mathbf {R} }},{\hat {\mathbf {n} }}})+{\frac {\partial \psi (\mathbf {r} ')}{\partial n'}}\right]\,\mathrm {d} S'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8a49a43adeb04912a7c2f3476821f660eec8ae9) 。
。
這是基爾霍夫繞射公式最廣義的形式。解析涉及到有限尺寸波源的問題,必須用體積分來將波源的每一點所給出的貢獻總合在一起。
光波是傳播於空間的電磁輻射,理當被視為一種電磁場向量現象。但是,基爾霍夫的理論是純量理論,將光波當作純量處理,這可能會造成偏差。因此,物理學者做了很多實驗來檢查結果是否準確。他們發現,只要孔徑尺寸比波長大很多、孔徑與觀察屏之間的距離不很近,則使用純量理論可以得到相當準確的答案。但是對於某些問題,例如高解像度光柵繞射,純量理論就不適用,必須使用向量理論。[5]
- ^ M. Born and E. Wolf, Principles of Optics, 1999, Cambridge University Press, Cambridge
- ^ RS Longhurst, Gemoetrical and Physical Optics, 1969, Longmans, London
- ^ 3.0 3.1 3.2 Hecht, Eugene. Optics 4th. United States of America: Addison Wesley. 2002: pp. 510–512. ISBN 0-8053-8566-5 (英語).
- ^ G. Kirchhoff, Ann. d. Physik. 1883, 2, 18, p663
- ^ Goodman, Joseph. Introduction to Fourier Optics 3rd. Roberts and Company Publishers. 2004: pp. 35. ISBN 978-0974707723.


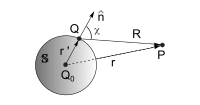

























![{\displaystyle \psi (\mathbf {r} )=-\ {\frac {i\psi _{0}}{2\lambda }}\oint _{\mathbb {S} }\left({\frac {e^{ik(r'+R)}}{r'R}}\right)[\cos \alpha +\cos \chi ]\,\mathrm {d} S'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95056bcf907df65cfb6994bcc5f3863cc3cf4729)







![{\displaystyle \psi (\mathbf {r} )={\frac {1}{4\pi }}\oint _{\mathbb {S} }\left[\psi (\mathbf {r} ')\nabla '\left({\frac {e^{ikR}}{R}}\right)-\left({\frac {e^{ikR}}{R}}\right)\nabla '\psi (\mathbf {r} ')\right]\cdot \,\mathrm {d} \mathbf {S} '}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8aa86dc8360be9cab45faab661ea3f9c06922c8)
![{\displaystyle \psi (\mathbf {r} )={\frac {1}{4\pi }}\oint _{\mathbb {S} }\left[\psi (\mathbf {r} '){\frac {\partial }{\partial n'}}\left({\frac {e^{ikR}}{R}}\right)-\left({\frac {e^{ikR}}{R}}\right){\frac {\partial \psi (\mathbf {r} ')}{\partial n'}}\right]\,\mathrm {d} S'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e96278c09f0fd019ee85b12fa33b7392584ca84c)








![{\displaystyle \psi (\mathbf {r} )={\frac {\psi _{0}}{4\pi }}\oint _{\mathbb {S} }\left[\left({\frac {e^{ikr'}}{r'}}\right)\nabla '\left({\frac {e^{ikR}}{R}}\right)-\left({\frac {e^{ikR}}{R}}\right)\nabla '\left({\frac {e^{ikr'}}{r'}}\right)\right]\cdot \,{\hat {\mathbf {n} }}\mathrm {d} S'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c759f4cb7ee95e5784775a7bbdfa5f519e4cf08)







![{\displaystyle [1+\cos(\chi )]/2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/295b98404bec9961d59e831cf2dcb29630143ad3)











![{\displaystyle {\begin{aligned}\psi (\mathbf {r} )&\approx -\ {\frac {i\psi _{0}}{2\lambda }}{\frac {e^{ik(r'+r)}}{r'r}}\int _{0}^{\pi }e^{-ikr'\cos(\theta )}[1+\cos(\theta )]2\pi r'^{2}\sin(\theta )\mathrm {d} \theta \\&\approx -\ {\frac {ik\psi _{0}r'e^{ik(r'+r)}}{2r}}\int _{0}^{\pi }e^{-ikr'\cos(\theta )}[1+\cos(\theta )]\sin(\theta )\mathrm {d} \theta \\&\approx -\ {\frac {ik\psi _{0}r'e^{ik(r'+r)}}{2r}}\ {\frac {2[\sin(kr')+i\cos(kr')]}{kr'}}\\&\approx \psi _{0}{\frac {e^{ikr}}{r}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcdbc9c562b92d47605d3873eb91626446079b18)

![{\displaystyle \psi (\mathbf {r} )=-\ {\frac {1}{4\pi }}\oint _{\mathbb {S} }\left({\frac {e^{ikR}}{R}}\right)\left[ik\psi (\mathbf {r} ')\cos {({\hat {\mathbf {R} }},{\hat {\mathbf {n} }}})+{\frac {\partial \psi (\mathbf {r} ')}{\partial n'}}\right]\,\mathrm {d} S'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8a49a43adeb04912a7c2f3476821f660eec8ae9)