菊池線 (物理)
菊池線(日語:菊池線/きくちせん,英語:Kikuchi lines)是電子散射形成的圖形。它們結合在一起形成單晶樣品的電子衍射帶,在那裡作為「定向空間的道路」,對於不確定他們所看到的是什麼。在透射電子顯微鏡中,它們很容易在樣品厚度足以進行多次散射的區域的衍射中被看到。[1]當晶體傾斜時,衍射點會忽亮忽暗,與此不同,菊池帶用明確定義的交叉點(稱為區域或極點)以及連接一個交叉點到下一個交叉點的路徑來標記方向空間。
菊池帶幾何的實驗和理論圖,以及它們的直接空間類似物,如彎曲輪廓、電子溝道模式和條紋可見性圖,在晶體和納米晶材料的電子顯微鏡學中越來越有用。[2]因為每條菊池線都與一組晶格平面的一側的布拉格衍射有關,所以這些線可以用相同的密勒指數或倒數晶格指數來標記,這些指數用來識別單個的衍射點。另一方面,菊池帶交點或區域用直接格指數來進行表示,即表示格基向量a、b和c的整數倍的表示方法。
菊池線是由散射的電子形成的衍射圖案,例如由於熱原子振動的結果。[3]它們的主要幾何特徵可以從菊池正士在1928年提出的一個簡單的彈性機制中推斷出來,[4]儘管需要用漫射非彈性散射的動力學理論來定量地理解它們。[5]
在X射線散射中,這些線被稱為科塞爾線[6](以瓦爾特·科塞爾的名字命名)。
記錄實驗中的菊池圖案和示意圖
[編輯]
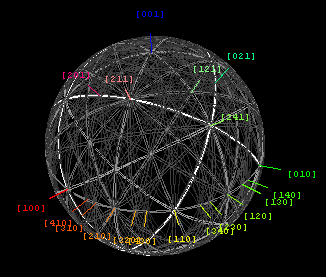
左邊的圖顯示了通向硅[100]區的菊池線,其光束方向離(004)菊池帶的區域約7.9度。在圖像的動態範圍是如此之大,只有部分膠片沒有過度曝光。對於適應黑暗環境的眼睛來說,在熒光屏上捕捉菊池線要比在紙上或膠片上捕捉靜止狀態要容易得多,儘管眼睛和攝影介質對光照強度都有大致對數的響應。因此,電荷耦合器件的大線性動態範圍有助於對這些衍射特徵進行充分的定量研究。[7]
這幅圖像對應的角度範圍超過10度,需要使用比通常的相機長度L更短的相機。菊池的帶寬本身(大約是倍角/d,其中倍角/d大約是對應平面布拉格角的兩倍)遠低於1度,因為電子的波長倍(在這種情況下大約是1.97皮)遠小于格點平面的d-間距本身。相比之下,硅(022)的d-間距約為192皮,而硅(004)的d-間距約為136皮。
該圖像取自晶體的一個區域,該區域比非彈性平均自由路徑(大約200納米)厚,因此漫射散射特徵(菊池線)與相干散射特徵(衍射點)相比會更強。倖存的衍射點出現在由明亮的菊池線相交的圓盤上,這一事實意味着衍射圖案是用會聚的電子束拍攝的。在實踐中,菊池線在選定區域或會聚束電子衍射圖案的厚區域很容易看到,但是在小於100納米的晶體的衍射中很難看到(在那裡晶格條紋的可見性效應變得很重要)。這個圖像是用會聚光束記錄的,因為會聚光束縮小了必須記錄在膠片上的對比度範圍。
編譯覆蓋範圍超過1個球面度的菊池圖像需要拍攝許多傾斜變化的圖像(例如在每個方向上變化2度)。這可能是一項乏味的工作,但在研究結構未知的晶體時可能有用,因為它可以清楚地揭示三維晶格的對稱性。[8]
菊池線示意圖及其立體投影
[編輯]

左邊的圖為硅的方向空間的更大的部分繪製了菊池線。底部的大[011]區和[001]區之間的夾角為45度。請注意,右下角的四重區(此處標記為[001])與上面實驗模式中標記為[100]的區域具有相同的對稱性和方向,儘管該實驗模式僅對10度左右。
還要注意的是,左邊的圖形是從以那個[001]區域為中心的立體投影中摘錄的。這種保角投影允許我們將球面映射到一個平面上,同時保持局部的交角,從而保持區域的對稱性。繪製這樣的圖需要一個人能夠畫出具有非常大曲率半徑的圓弧。例如,左邊的圖形是在計算機出現之前畫的,因此需要使用長臂圓規。如今,找到一個長臂圓規可能相當困難,因為在計算機的幫助下,繪製具有較大曲率半徑(二維或三維)的曲線要容易得多。
立體圖的保角效果在右圖中更為明顯,它對面心晶體或立方緻密晶體(如金或鋁)的取向空間進行了整整180度的傾斜。動畫遵循<111>區域之間的面心立方晶體的{220}流蘇可見帶,在該點旋轉60度設置旅行通過重複原始序列到下一個<111>區域。邊緣-可見帶與菊池帶具有相同的全局幾何結構,但是對於較薄的樣本,它們的寬度與d間距成比例(而不是反比)。雖然用菊池帶實驗獲得的角場寬度(和傾斜範圍)通常要小得多,但動畫提供了一個廣角視圖,說明菊池帶如何幫助有見識的晶體學家在單個晶體標本的方向空間中找到標示。
真實空間類似物
[編輯]
在較厚的樣品的衍射圖像中,菊池線用來突出晶格面上的邊緣。由於高能電子衍射中的布拉格角非常小(300 keV時約為1⁄4度),菊池帶在倒數空間中相當狹窄。這也意味着在真實空間圖像中,晶格平面的邊緣不是由漫射散射特徵裝飾的,而是與相干散射相關聯的。這些相干散射特性包括添加衍射(負責彎曲輪廓曲線箔),更多的電子滲透(產生電子在晶體表面的掃描電子圖像引導模式),和晶格條紋反差(結果依賴的晶格條紋強度梁取向與試樣厚度)。雖然細節對比不同,但這些特徵的格平面軌跡幾何與菊池圖是相同的。
彎曲輪廓和搖擺曲線
[編輯]
搖擺曲線(左)[9]是散射電子強度的圖,它是入射電子束與樣品中一組晶格平面法線夾角的函數。當這個角度從側面(在這個方向上,電子束平行於晶格平面並垂直於它們的法線)向任何方向改變時,光束進入布拉格衍射狀態,更多的電子在顯微鏡的後焦平面孔徑外被衍射,產生如圖中所示的彎曲硅箔所示的黑線對帶。
[100]這幅圖的彎曲輪廓「蜘蛛」被困在一個硅的區域中,硅的形狀像一個橢圓形的手錶玻璃,尺寸小於一微米,用300 keV電子成像。如果你傾斜水晶,蜘蛛移動到橢圓形的邊緣,好像它試圖出去。例如,在這幅圖像中,當樣本向左傾斜時,蜘蛛的[100]交叉點移到了橢圓的右邊。
「蜘蛛」的腿和它們的交叉點可以被索引,就像上面關於實驗性菊池圖案的章節中接近[100]的菊池圖案一樣。原則上,我們可以使用這個彎曲輪廓來模擬箔片在橢圓上所有點上的矢量傾斜(毫弧度精度)。
格狀條紋可見度圖
[編輯]從上面的搖擺曲線可以看出,隨着試樣厚度為10納米和小範圍(例如300 keV附近電子和晶格間距0.23海里)傾斜的角度範圍,產生衍射和/或晶格條紋對比試樣厚度成反比。因此,晶格條紋的幾何形狀在納米材料的電子顯微鏡研究中非常有用,[10][11]正如彎曲輪廓線和菊池線在研究單晶樣品(例如厚度在10微米範圍內的金屬和半導體樣品)中很有用一樣。例如,納米結構的應用包括:(i)從不同傾斜度下拍攝的圖像中確定單個納米顆粒的三維晶格參數,[12](ii)隨機取向的納米顆粒採集的條紋指紋,(iii)基於傾斜度下條紋對比度變化的顆粒厚度圖,(iv)從隨機取向的納米顆粒晶格圖像中檢測二十面體孿晶,(v)分析納米顆粒與圓柱支架的取向關係。
電子溝道圖
[編輯]
上述技術都涉及檢測電子通過一個薄標本,通常在透射電子顯微鏡。另一方面,掃描電子顯微鏡,當一個聚焦的電子束光柵穿過一個厚的標本時,典型的觀察電子「被激活」。電子溝道模式是在掃描電子顯微鏡次級和/或背散射電子圖像中顯示的與邊緣晶格平面相關的對比效應。
對比效應與彎曲等高線相似,即在衍射條件下進入晶體表面的電子傾向於通過通道(在不損失能量的情況下更深入地穿透試件),從而在靠近進入表面處激發更少的電子進行探測。因此,條帶的形成取決於光束/晶格的方向,與現在熟悉的菊池線幾何。
第一張掃描電子顯微鏡(SEM)圖像是硅鋼的電子溝道造影。[13]然而,這種技術的實際應用是有限的,因為通常只有一層薄薄的磨損損傷或非晶塗層就足以模糊對比度。[14]如果標本在檢查前必須塗上一層導電塗層以防止充電,這也會模糊對比。在切割表面和原子尺度上自組裝的表面上,電子溝道模式很可能在未來幾年在現代顯微鏡上得到越來越多的應用。
另見
[編輯]參考文獻
[編輯]- ^ David B. Williams; C. Barry Carter. Transmission electron microscopy: A textbook for materials science
 . Plenum Press, NY. 1996. ISBN 978-0-306-45324-3.
. Plenum Press, NY. 1996. ISBN 978-0-306-45324-3.
- ^ K. Saruwatari; J. Akai; Y. Fukumori; N. Ozaki; H. Nagasawa; T. Kogure. Crystal orientation analyses of biominerals using Kikuchi patterns in TEM. J. Mineral. Petrol. Sci. 2008, 103: 16–22.
- ^ Earl J. Kirkland. Advanced computing in electron microscopy. Plenum Press, NY. 1998: 151. ISBN 978-0-306-45936-8.
- ^ S. Kikuchi. Diffraction of Cathode Rays by Mica. Japanese Journal of Physics. 1928, 5 (3061): 83–96. Bibcode:1928Natur.121.1019N. doi:10.1038/1211019a0.
- ^ P. Hirsch; A. Howie; R. Nicholson; D. W. Pashley; M. J. Whelan. Electron microscopy of thin crystals. Butterworths/Krieger, London/Malabar FL. 1977. ISBN 978-0-88275-376-8.
- ^ R. W. James. Chapter VIII. The Optical Principles of the Diffraction of X-Rays'. Ox Bow Press, Woodbridge, Connecticut. 1982. ISBN 978-0-918024-23-7.
- ^ J. C. H. Spence and J. Zuo. Ch. 9. Electron microdiffraction. Plenum, New York. 1992. ISBN 978-0-306-44262-9.
- ^ E. Levine; W. L. Bell; G. Thomas. Further applications of Kikuchi diffraction patterns; Kikuchi maps. Journal of Applied Physics. 1966, 37 (5): 2141–2148. Bibcode:1966JAP....37.2141L. doi:10.1063/1.1708749.
- ^ H. Hashimoto; A. Howie; M. J. Whelan. Anomalous Electron Absorption Effects in Metal Foils: Theory and Comparison with Experiment. Proceedings of the Royal Society A. 1962, 269 (1336): 80. Bibcode:1962RSPSA.269...80H. doi:10.1098/rspa.1962.0164.
- ^ P. Fraundorf; Wentao Qin; P. Moeck; Eric Mandell. Making sense of nanocrystal lattice fringes. Journal of Applied Physics. 2005, 98 (11): 114308–114308–10. Bibcode:2005JAP....98k4308F. arXiv:cond-mat/0212281
 . doi:10.1063/1.2135414.
. doi:10.1063/1.2135414.
- ^ P. Wang; A. L. Bleloch; U. Falke; P. J. Goodhew. Geometric aspects of lattice contrast visibility in nanocrystalline materials using HAADF STEM. Ultramicroscopy. 2006, 106 (4–5): 277–283. doi:10.1016/j.ultramic.2005.09.005.
- ^ Wentao Qin; P. Fraundorf. Lattice parameters from direct-space images at two tilts. Ultramicroscopy. 2003, 94 (3–4): 245–262. PMID 12524195. arXiv:cond-mat/0001139
 . doi:10.1016/S0304-3991(02)00335-2.
. doi:10.1016/S0304-3991(02)00335-2.
- ^ Knoll M. Aufladepotentiel und sekundäremission elektronenbestrahlter körper (Static potential and secondary emission of bodies under electron irradiation). Z. Tech. Phys. 1935, 11: 467–475.
- ^ J. I. Goldstein; D. E. Newbury; P. Echlin; D. C. Joy; A. D. Romig Jr.; C. E. Lyman; C. Fiori; E. Lifshin. Scanning electron microscopy and X-ray microanalysis. Plenum Press, NY. 1992. ISBN 978-0-306-44175-2.
