帕松光斑

在帕松光斑實驗裏，點光源照射在一個圓形物體，因而在屏幕形成陰影。在陰影的中心會出現一粒明亮光點，這是因為衍射而產生的現象，這證實了波動光學的預言。

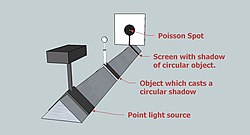
泊松光斑，也稱阿拉戈光斑。是一種由於光的衍射而產生的一種光學現象。

在滿足菲涅耳數的情況下：

$F={\frac {d^{2}}{\ell \lambda }}\gtrsim 1$

其中

d是圓形遮蔽物的直徑

ℓ是遮蔽物到屏幕的距離

λ是光源的波長

當單色光照射在一定尺寸的小圓板或圓珠時，會在之後的光屏上出現環狀的互為同心圓的衍射條紋，並且在所有同心圓的圓心處會出現一個極小的亮斑，這個亮斑就被稱為泊松亮斑。這個亮斑的出現是對光的波動性的一個很好的證明。

有趣的是，雖然這個現象是由最早計算得到它的法國物理學家西莫恩·泊松命名，但泊松卻是企圖利用「中心點的光穿過障礙物到達光屏」這個與常識相違背的結論來推翻光的波動說。

除光外，在其他物質流的衍射現象中也能發現泊松亮斑的存在。

歷史

1814年，奧古斯丁·菲涅耳開始致力於光的本性的研究，他再度重現了托馬斯·楊於1801年建立的光的雙縫干涉實驗，並用惠更斯原理對這一現象作出完美的解釋。與此同時，他開始研究小孔衍射問題。

1817年，法蘭西學術院舉行了一次關於光的本性問題的科研成果最佳論文競賽，菲涅耳加緊了研究工作；他在他弟弟的幫助下，成功地提出了後人稱之為惠更斯－菲涅耳原理，他用這一原理出色地解釋了光的直線傳播規律，提出了光的衍射理論的子波解釋，並於1818年提交了論文。科學院成立了一個評委會，評委會的成員中有波動的支持者弗朗索瓦·阿拉戈（1786—1853），有波動說的反對者泊松（1781—1840）、讓-巴蒂斯特·畢奧（1774—1862）、皮埃爾-西蒙·拉普拉斯（1749—1827），有一中立者路易斯·蓋-呂薩克（1778—1850）。儘管不少成員不相信菲涅耳的觀念，但是最終還是被菲涅耳數學上的巨大成功及其與實驗上的一致性所征服，並授予他優勝獎。

泊松想推翻菲涅耳的觀點，就藉助於波動理論對衍射理論進行詳細地分析。他發現：用一個圓片作為遮擋物時。光屏的中心應出現一個亮點（或者用圓孔做實驗時，應該在光屏的中心出一個暗斑），這是令人難以相信的事實，過去也未曾有人見到過。菲涅耳又經過嚴密的數學計算發現，只有當這個圓片的半徑很小時，這個亮點才比較明顯（或圓孔很小時，暗斑明顯）。事後，菲涅耳和阿拉戈精心設計了一個實驗，確認了這一亮斑的存在，證明了這一預言的正確性。

這個初看起來似乎是荒謬的結論，是泊松研究菲涅耳論文時把它當作謬誤提出來的，但卻成了支持波動說的強有力的證據。後來人們為了紀念這一極具戲劇性事實，就把衍射光斑中央出現的亮斑（或暗斑）稱為「泊松光斑」。

參閱

• 基爾霍夫積分定理