準晶體

準晶體,亦稱為「准晶」或「擬晶」,是一種介於晶體和非晶體之間的固體。准晶體具有與晶體相似的長程有序的原子排列;但是准晶體不具備晶體的平移對稱性。根據晶體局限定理(crystallographic restriction theorem),普通晶體只能具有二次、三次、四次或六次旋轉對稱性,但是准晶的布拉格衍射圖具有其他的對稱性,例如五次對稱性或者更高的如六次以上的對稱性。
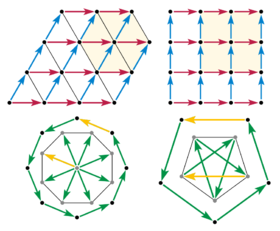
兼容:六次(三次)、4次(二次);
不兼容: 八次、五次。
數學家在20世紀60年代就發現了這種非週期平鋪圖形。但是直到快20年後這種理論上的結構才和准晶的研究聯繫起來。自然界中非周期圖形的發現在結晶學領域造成了典範轉移。雖然准晶體在此前就已被觀察到並被研究[1],但由於它們違背了人們之前對於晶體結構的認識,所以直至20世紀80年代才開始受到重視。
獲得2011年諾貝爾化學獎的丹·舍特曼是第一個正式報道發現了准晶的人。1984年他和以色列理工學院的同事們在快速冷卻的鋁錳合金中發現了一種新的金屬相,其電子衍射斑具有明顯的五次對稱性。這篇文章發表於物理評論快報(Physical Review Letters)上。
歷史
[編輯]
准晶體的結構在20世紀之前就已經被建築師熟知,例如在伊朗伊斯法罕的清真寺,上面瓷磚的圖案就是按照准晶樣式排列。[2]
1961年,數學家王浩提出了用不同形狀的拼圖鋪滿平面的拼圖問題。數學家們已經知道,可以用單一形狀的拼圖拼滿一個平面,例如任意形狀的四邊形或者正六邊形,但是當增加拼圖單元的種類時,就能夠構造出更多的拼滿一個平面的方法。兩年後,王浩的學生Robert Berger構造了一系列不具有周期性的拼圖方法。之後鋪滿平面所需要的拼圖種類越來越少,1976年羅傑·潘洛斯(Roger Penrose)構造了一系列只需要兩種拼圖的方法,這種方法拼出來的圖案具有五次對稱性。
之後丹尼爾·舍特曼發現了三維世界中的20面體准晶。這一準晶的拼圖形式由兩種不同的菱形組成。這篇文章發表於1984年,標題為「一種長程有序但是不具有平移對稱性的金屬相」(Metallic Phase with Long-Range Orientational Order and No Translational Symmetry)。他們發現的這一五次對稱性結構產生於融化後快速冷卻的Al-Mn合金中。[3]

第二年Ishimasa等人報道了Ni-Cr顆粒中的十二次對稱性。之後在V-Ni-Si和Cr-Ni-Si合金中又發現了八次對稱衍射圖。[4][5]多年以來已經發現了幾百種具有多種組成和對稱性的准晶體。最早發現的這種准晶體結構在熱力學上是不穩定的,一旦加熱就會重新變成規則晶體。但是1987年的時候發現了許多種穩定的准晶體,這樣就可以合成更大的晶體用於進一步的結構及應用研究。
2009年,礦物學上的一個發現為準晶是否能在自然條件下形成提供了證據:[6]俄羅斯的一塊鋁鋅銅礦上發現了Al63Cu24Fe13組成的准晶顆粒。和實驗室中合成的一樣,這些顆粒的結晶程度都非常好。[7]
原理
[編輯]一種典型的準晶體結構是三維空間的彭羅斯拼圖(Penrose)。二維空間的彭羅斯拼圖由內角為36度、144度和72度、108度的兩種菱形組成,能夠無縫隙無交疊地排滿二維平面。這種拼圖沒有平移對稱性,但是具有長程的有序結構,並且具有晶體所不允許的五次旋轉對稱性。
準晶體是其中原子的排列存在5次和6次以上對稱軸的一種特殊的晶體。它既不同於非晶體,也不同於真正完整的晶體。晶體為具有平移對稱的固體,即整個晶體中原子的排列都是很規則。三維晶體不可能具有5次和6次以上的對稱軸,此點可由晶體學限制定理證明。而准晶體是無平移對稱性但長程有序的固體,即在大範圍內原子的排列是規則(有序)的,因此其電子衍射圖仍具有明銳衍射斑。
參見
[編輯]參考資料
[編輯]- ^ Steurer W., Z. Kristallogr. Twenty years of structure research on quasicrystals. Part 1. Pentagonal, octagonal, decagonal and dodecagonal quasicrystals. Zeitschrift für Kristallographie. 2004, 219 (7): 391-446. doi:10.1524/zkri.219.7.391.35643 (英語).[永久失效連結]
- ^ Lu, P. J.; Steinhardt, P. J. Decagonal and Quasi-Crystalline Tilings in Medieval Islamic Architecture. Science. 2007, 315 (5815): 1106–1110. Bibcode:2007Sci...315.1106L. PMID 17322056. doi:10.1126/science.1135491.
- ^ Kramer, P.; Neri, R. On periodic and non-periodic space fillings of E(m) obtained by projection. Acta Crystallographica. 1984, A40 (5): 580. doi:10.1107/S0108767384001203.
- ^ Ishimasa, T.; Nissen, H.-U.; Fukano, Y. New ordered state between crystalline and amorphous in Ni-Cr particles. Physical Review Letters. 1985, 55 (5): 511–513. Bibcode:1985PhRvL..55..511I. PMID 10032372. doi:10.1103/PhysRevLett.55.511.
- ^ Wang, N.; Chen, H.; Kuo, K. Two-dimensional quasicrystal with eightfold rotational symmetry. Physical Review Letters. 1987, 59 (9): 1010–1013. Bibcode:1987PhRvL..59.1010W. PMID 10035936. doi:10.1103/PhysRevLett.59.1010.
- ^ Bindi, L.; Steinhardt, P. J.; Yao, N.; Lu, P. J. Natural Quasicrystals. Science. 2009, 324 (5932): 1306–9. Bibcode:2009Sci...324.1306B. PMID 19498165. doi:10.1126/science.1170827.
- ^ Steinhardt, Paul; Bindi, Luca. Once upon a time in Kamchatka: the search for natural quasicrystals. Philosophical Magazine. 2010: 1 [2011-10-05]. doi:10.1080/14786435.2010.510457. (原始內容存檔於2011-09-27).