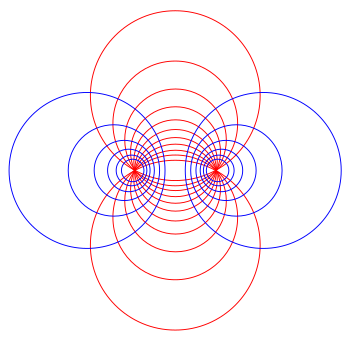
双极坐标系绘图。图中的红色圆圈是
σ
{\displaystyle \sigma }
τ
{\displaystyle \tau }
双极圆柱坐标系 (英语:Bipolar cylindrical coordinates )是一种三维正交坐标系 。往 z-轴方向延伸二维的双极坐标系 ,则可得到双极圆柱坐标系。双极坐标系的两个焦点
F
1
{\displaystyle F_{1}}
F
2
{\displaystyle F_{2}}
直角坐标
(
x
,
y
)
{\displaystyle (x,\ y)}
(
−
a
,
0
)
{\displaystyle (-a,\ 0)}
(
a
,
0
)
{\displaystyle (a,\ 0)}
L
1
{\displaystyle L_{1}}
L
2
{\displaystyle L_{2}}
焦线 。
双极圆柱坐标
(
σ
,
τ
,
z
)
{\displaystyle (\sigma ,\ \tau ,\ z)}
x
=
a
sinh
τ
cosh
τ
−
cos
σ
{\displaystyle x=a\ {\frac {\sinh \tau }{\cosh \tau -\cos \sigma }}}
y
=
a
sin
σ
cosh
τ
−
cos
σ
{\displaystyle y=a\ {\frac {\sin \sigma }{\cosh \tau -\cos \sigma }}}
z
=
z
{\displaystyle z=z}
其中,点
P
{\displaystyle P}
σ
{\displaystyle \sigma }
∠
F
1
P
F
2
{\displaystyle \angle F_{1}PF_{2}}
τ
{\displaystyle \tau }
d
1
=
F
1
P
{\displaystyle d_{1}=F_{1}P}
d
2
=
F
2
P
{\displaystyle d_{2}=F_{2}P}
自然对数
τ
=
ln
d
1
d
2
{\displaystyle \tau =\ln {\frac {d_{1}}{d_{2}}}}
注意到焦线
F
1
{\displaystyle F_{1}}
F
2
{\displaystyle F_{2}}
x
=
−
a
{\displaystyle x=-a}
x
=
a
{\displaystyle x=a}
双极坐标的几何诠释。
F
1
P
¯
{\displaystyle {\overline {F_{1}P}}}
F
2
P
¯
{\displaystyle {\overline {F_{2}P}}}
∠
F
1
P
F
2
{\displaystyle \angle F_{1}PF_{2}}
σ
{\displaystyle \sigma }
F
1
P
{\displaystyle F_{1}P}
F
2
P
{\displaystyle F_{2}P}
自然对数 是
τ
{\displaystyle \tau }
σ
{\displaystyle \sigma }
τ
{\displaystyle \tau }
不同
σ
{\displaystyle \sigma }
坐标曲面 是一组不同圆心线,而相交于两个焦线
L
1
{\displaystyle L_{1}}
L
2
{\displaystyle L_{2}}
x
2
+
(
y
−
a
cot
σ
)
2
=
a
2
sin
2
σ
{\displaystyle x^{2}+(y-a\cot \sigma )^{2}={\frac {a^{2}}{\sin ^{2}\sigma }}}
它们的圆心线都包含于 yz-平面。正值
σ
{\displaystyle \sigma }
y
>
0
{\displaystyle y>0}
σ
{\displaystyle \sigma }
y
<
0
{\displaystyle y<0}
|
σ
|
{\displaystyle \left|\sigma \right|}
|
σ
|
{\displaystyle \left|\sigma \right|}
π
/
2
{\displaystyle \pi /2}
不同
τ
{\displaystyle \tau }
坐标曲面 是一组围著焦线,互不相交,不同半径的圆柱面。半径为
y
2
+
(
x
−
a
coth
τ
)
2
=
a
2
sinh
2
τ
{\displaystyle y^{2}+\left(x-a\coth \tau \right)^{2}={\frac {a^{2}}{\sinh ^{2}\tau }}}
它们的圆心线都包含于 xz-平面。正值
τ
{\displaystyle \tau }
x
>
0
{\displaystyle x>0}
τ
{\displaystyle \tau }
x
<
0
{\displaystyle x<0}
τ
=
0
{\displaystyle \tau =0}
τ
{\displaystyle \tau }
双极圆柱坐标
(
σ
,
τ
,
z
)
{\displaystyle (\sigma ,\ \tau ,\ z)}
(
x
,
y
,
z
)
{\displaystyle (x,\ y,\ z)}
d
1
2
=
(
x
+
a
)
2
+
y
2
{\displaystyle d_{1}^{2}=(x+a)^{2}+y^{2}}
d
2
2
=
(
x
−
a
)
2
+
y
2
{\displaystyle d_{2}^{2}=(x-a)^{2}+y^{2}}
τ
{\displaystyle \tau }
d
1
{\displaystyle d_{1}}
d
2
{\displaystyle d_{2}}
自然对数 :
τ
=
ln
d
1
d
2
{\displaystyle \tau =\ln {\frac {d_{1}}{d_{2}}}}
∠
F
1
P
F
2
{\displaystyle \angle F_{1}PF_{2}}
F
1
P
¯
{\displaystyle {\overline {F_{1}P}}}
F
2
P
¯
{\displaystyle {\overline {F_{2}P}}}
σ
{\displaystyle \sigma }
馀弦定理 来计算:
cos
σ
=
d
1
2
+
d
2
2
−
4
a
2
2
d
1
d
2
{\displaystyle \cos \sigma ={\frac {d_{1}^{2}+d_{2}^{2}-4a^{2}}{2d_{1}d_{2}}}}
z-坐标的公式不变:
z
=
z
{\displaystyle z=z}
双极圆柱坐标
σ
{\displaystyle \sigma }
τ
{\displaystyle \tau }
z
{\displaystyle z}
h
σ
=
h
τ
=
a
cosh
τ
−
cos
σ
{\displaystyle h_{\sigma }=h_{\tau }={\frac {a}{\cosh \tau -\cos \sigma }}}
h
z
=
1
{\displaystyle h_{z}=1}
所以,无穷小体积元素等于
d
V
=
a
2
(
cosh
τ
−
cos
σ
)
2
d
σ
d
τ
d
z
{\displaystyle dV={\frac {a^{2}}{\left(\cosh \tau -\cos \sigma \right)^{2}}}d\sigma d\tau dz}
拉普拉斯算子 是
∇
2
Φ
=
1
a
2
(
cosh
τ
−
cos
σ
)
2
(
∂
2
Φ
∂
σ
2
+
∂
2
Φ
∂
τ
2
)
+
∂
2
Φ
∂
z
2
{\displaystyle \nabla ^{2}\Phi ={\frac {1}{a^{2}}}\left(\cosh \tau -\cos \sigma \right)^{2}\left({\frac {\partial ^{2}\Phi }{\partial \sigma ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \tau ^{2}}}\right)+{\frac {\partial ^{2}\Phi }{\partial z^{2}}}}
其它微分算子,例如
∇
⋅
F
{\displaystyle \nabla \cdot \mathbf {F} }
∇
×
F
{\displaystyle \nabla \times \mathbf {F} }
正交坐标系 的一般方程式内。
双极圆柱坐标有一个经典的应用,这是在解析像拉普拉斯方程 或亥姆霍兹方程 这类的偏微分方程式 。在这些方程式里,双极圆柱坐标允许分离变数法 的使用。一个典型的例题是,有两个互相平行的圆柱导体 ,请问其周围的电场 为什么?应用双极圆柱坐标,我们可以精致地分析这例题。
Margenau H, Murphy GM. The Mathematics of Physics and Chemistry. New York: D. van Nostrand. 1956: pp. 187–190. Korn GA, Korn TM. Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. 1961: p. 182. ASIN B0000CKZX7. Moon P, Spencer DE. Conical Coordinates (r, θ, λ). Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions corrected 2nd ed., 3rd print ed. New York: Springer-Verlag. 1988: unknown. ISBN 978-0387184302