阻抗

用以展示复阻抗的相量图。

阻抗（英语：Electrical impedance）又称电阻抗，是电路中电阻、电感、电容对交流电的阻碍作用的统称。阻抗是一个复数，实部称为电阻，虚部称为电抗；其中电容在电路中对交流电所起的阻碍作用称为容抗，电感在电路中对交流电所起的阻碍作用称为感抗，容抗和感抗合称为电抗。阻抗将电阻的概念加以延伸至交流电路领域，不仅描述电压与电流的相对振幅，也描述其相对相位。当通过电路的电流是直流电时，电阻与阻抗相等，电阻可以视为相位为零的阻抗。阻抗的概念不仅存在于电路中，在力学的振动系统中也有涉及。

阻抗通常以符号 $Z$ 标记。阻抗是复数，可以用相量 $Z_{m}\angle \theta$ 或 $Z_{m}e^{j\theta }$ 来表示；其中，$Z_{m}$是阻抗的大小，$\theta$ 是阻抗的相位。这种表示法称为“相量表示法”。

具体而言，阻抗定义为电压与电流的频域比率。阻抗的大小 $Z_{m}$ 是电压振幅与电流振幅的绝对值比率，阻抗的相位 $\theta$ 是电压与电流的相位差。采用国际单位制，阻抗的单位是欧姆（Ω），与电阻的单位相同。阻抗的倒数是导纳，即电流与电压的频域比率。导纳的单位是西门子（旧单位是姆欧）。

词源

英文术语“impedance”是由物理学者奥利弗·黑维塞于1886年发表论文《电工》给出。1893年，电机工程师亚瑟·肯乃利（Arthur Kennelly）最先以复数表示阻抗。

1927年，孔祥鹅《商榷电机工程译名问题》一文建议采用“电阻抗”作为该术语中文译名，以便顾及与“电抗”（electrical reactance）、“电阻”（electrical resistance）二词的学理关联。这一译名得以沿用至今。

复阻抗

阻抗是复数，可以与术语“复阻抗”替换使用。阻抗通常以相量来表示，这种表示法称为“相量表示法”。相量有三种等价形式：

1. 直角形式：$R+jX$ 、
2. 极形式：$Z_{m}\angle \theta$ 、
3. 指数形式：$Z_{m}e^{j\theta }$ ；

其中，电阻 $R$ 是阻抗的实部，电抗 $X$ 是阻抗的虚部，$Z_{m}$ 是阻抗的大小，$j$ 是虚数单位，$\theta$ 是阻抗的相位。

从指数形式转换到直角形式可以使用方程式

$R=Z_{m}\cos \theta$ 、

$X=Z_{m}\sin \theta$ 。

从直角形式转换到指数形式可以使用方程式

$Z_{m}={\sqrt {R^{2}+X^{2}}}$ 、

$\theta =\arctan(X/R)$ 。

极形式适用于实际工程标示，而直角形式比较适用于几个阻抗相加或相减的案例，指数形式则比较适用于几个阻抗相乘或相除的案例。在作电路分析时，例如在计算两个阻抗并联的总阻抗时，可能会需要作几次形式转换。这种形式转换必需要依照复数转换定则。

欧姆定律

连接于电路的交流电源会给出电压 $v(t)$ 于负载 $Z$ 的两端，并且驱动电流 $i(t)$ 于电路。

主条目：欧姆定律

藉著欧姆定律，可以了解阻抗的内涵：

$v=iZ=iZ_{m}e^{j\theta }$ 。

阻抗大小 $Z_{m}$ 的作用恰巧就像电阻，设定电流 $i$ ，就可计算出阻抗 $Z$ 两端的电压降 $v$ 。相位因子 $e^{j\theta }$ 则是电流滞后于电压的相位差 $\theta$ （在时域，电流信号会比电压信号慢 $\theta T/2\pi$ 秒；其中， $T$ 是单位为秒的周期）。

就像电阻将欧姆定律延伸至交流电路领域，其它直流电路分析的结果，例如电压分配（voltage division）、电流分配（current division）、戴维宁定理、诺顿定理等等，都可以延伸至交流电路领域，只需要将电阻更换为阻抗就行了。

复值电压与电流

电路内的广义阻抗可以描绘为与电阻符号相同的形状，或者描绘为加有标签的盒子。

为了简化计算，正弦电压波 $v(t)$ 和正弦电流波 $i(t)$ 通常以指数形式表示为

$v(t)=V_{m}e^{j(\omega t+\phi _{V})}$ 、

$i(t)=I_{m}e^{j(\omega t+\phi _{I})}$ ；

其中，$V_{m}>0$ 是电压振幅，$I_{m}>0$ 是电流振幅，$\omega$ 是正弦波的角频率、$\phi _{V}$ 是电压相位，$\phi _{I}$ 是电流相位，

阻抗定义为电压除以电流：

$Z\ {\stackrel {def}{=}}\ {\frac {v(t)}{i(t)}}$ 。

将这公式代入欧姆定律，可以得到

${\begin{aligned}V_{m}e^{j(\omega t+\phi _{V})}&=I_{m}e^{j(\omega t+\phi _{I})}Z_{m}e^{j\theta }\\&=I_{m}Z_{m}e^{j(\omega t+\phi _{I}+\theta )}\\\end{aligned}}$ 。

注意到对于任意时间 $t$ ，这方程式都成立。因此，可以令大小与相位分别相等：

$V_{m}=I_{m}Z_{m}$ 、

$\ \phi _{V}=\phi _{I}+\theta$ 。

第一个方程式乃是熟悉的表达电压与电流之间关系的欧姆定律，第二个方程式给出相位关系。

用相量表示法来描述，相量 $V$ 、$I$ 分别为

$V=V_{m}e^{j\phi _{V}}$ 、

$I=I_{m}e^{j\phi _{I}}$ 。

正弦波 $v(t)$ 、$i(t)$ 跟相量 $V$ 、$I$ 的关系为

$v(t)=Ve^{j\omega t}$ 、

$i(t)=Ie^{j\omega t}$ 。

阻抗的定义为

$Z\ {\stackrel {def}{=}}\ {\frac {V}{I}}$ 。

复数运算的正确性

根据欧拉公式，馀弦函数可以表示为

$\cos(\omega t+\phi )={\frac {1}{2}}{\Big [}e^{j(\omega t+\phi )}+e^{-j(\omega t+\phi )}{\Big ]}$ 。

这是一个可以用来表示电压或电流波形的实值馀弦函数，可以被分解为两个复值函数。所以，只要分析方程式右边的两个复值项目的行为，就可以明了方程式左边的实值馀弦函数的行为。由于这两个复值项目的实部相等，实际而言，只需要分析其中一个项目，取这项目的实部，就可以得到馀弦函数：

$\cos(\omega t+\phi )=\mathrm {Re} {\Big \{}e^{j(\omega t+\phi )}{\Big \}}$ 。

换句话说，只要取计算结果的实部，就可以得到答案。

在傅立叶分析中，激励可以写成多个正弦波的叠加。根据叠加原理，每个正弦波可以单独分析计算出各自的反应，（反应本身也是一个正弦波，其频率与激励的频率相同，但通常两者的振幅、相位都不相同，反应的振幅、相位会有所改变。）对于原本激励的响应是所有单独正弦波的响应在时域的总和（或积分）。这些单独正弦波都可以转换为以复数运算。

相量

主条目：相量

相量是一个常定复数，可以代表参数为时间的正弦函数的复振幅（大小和相位）。电机工程师常会使用相量作复数运算，因为能够简化涉及正弦函数的运算，将一个微分方程式问题约化为代数方程式问题。

一个电路元件的阻抗可以定义为元件两端的电压相量与通过元件的电流相量，两者之间的比率，即电压与电流之间的相对振幅与相对相位。注意到因子 $e^{j\omega t}$ 互相抵消，这定义等价于前面由欧姆定律给出的定义，

电路元件的阻抗

电容器两端的电压滞后于通过电容器的电流，两者之间的相位差为 $\pi /2$ ；电感器两端的电压超前于通过电感器的电流，两者之间的相位差为 $\pi /2$ 。由于电压与电流的振幅相等，阻抗的大小为1。

理想电阻器的阻抗 $Z_{R}$ 是实数，称为“电阻”：

$Z_{R}=R$ ；

其中，$R$ 是理想电阻器的电阻。

理想电容器和理想电感器的阻抗 $Z_{C}$ 、$Z_{L}$ 都是虚数 ：

$Z_{C}={\frac {1}{j\omega C}}$ ，

$Z_{L}=j\omega L$ ；

其中，$C$ 是理想电容器的电容，$L$ 是理想电感器的电感。

注意到以下两个很有用的全等式：

$j=e^{j\pi /2}$ 、

$-j=e^{-j\pi /2}$ 。

应用这些全等式，理想电容器和理想电感器的阻抗以指数形式重写为

$Z_{C}={\frac {e^{-j\pi /2}}{\omega C}}$ 、

$Z_{L}=\omega Le^{j\pi /2}$ 。

给定通过某阻抗元件的电流振幅，复阻抗的大小给出这阻抗元件两端的电压振幅，而复阻抗的指数因子则给出相位关系。

电阻器、电容器和电感器是三种基本电路元件。以下段落会推导出这些元件的阻抗。这些导引假定正弦信号。通过傅立叶分析，任意信号可以视为一组正弦函数的总和。所以，这些导引可以延伸至任意信号。

电阻器

根据欧姆定律，通过电阻器的含时电流 $i_{R}(t)$ 与电阻器两端的含时电压 $v_{R}(t)$ ，两者之间的关系为

$v_{R}(t)=i_{R}(t)R$ ；

其中，$t$ 是时间。

设定含时电压信号为

$v_{R}(t)=V_{0}\cos(\omega t)=V_{0}e^{j\omega t},\qquad V_{0}>0$ ，　

则含时电流为

$i_{R}(t)={\frac {V_{0}}{R}}e^{j\omega t}$ 。

两者的大小分别为 $V_{0}$ 、$V_{0}/R$ ，相位都是 $\omega t$ 。所以，阻抗为

$Z_{R}=R$ 。

电阻器的阻抗是实数。理想电阻器不会制造相位差。

电容器

通过电容器的含时电流 $i_{C}(t)$ 与电容器两端的含时电压 $v_{C}(t)$ ，两者之间的关系为

$i_{C}(t)=C{\frac {\operatorname {d} v_{C}(t)}{\operatorname {d} t}}$ 。

设定含时电压信号为

$v_{C}(t)=V_{0}\sin(\omega t)=\operatorname {Re} \{V_{0}e^{j(\omega t-\pi /2)}\}=\operatorname {Re} \{V_{C}e^{j\omega t}\},\quad where\quad V_{0}>0,\quad V_{C}=V_{0}e^{j(-\pi /2)}$ ，

则电流为

$i_{C}(t)=\omega V_{0}C\cos(\omega t)=\operatorname {Re} \{\omega V_{0}Ce^{j\omega t}\}=\operatorname {Re} \{I_{C}e^{j\omega t}\}$ 。

两者的除商为

${\frac {v_{C}(t)}{i_{C}(t)}}={\frac {V_{0}\sin(\omega t)}{\omega V_{0}C\cos(\omega t)}}={\frac {\sin(\omega t)}{\omega C\sin \left(\omega t+{\frac {\pi }{2}}\right)}}$ 。　

所以，电容器阻抗的大小为 $1/\omega C$ ，交流电压滞后90°于交流电流，或者，交流电流超前90°于交流电压。

以相量形式表示，

$V_{C}=V_{0}e^{j(-\pi /2)},\qquad V_{0}>0$ 、

$I_{C}=\omega V_{0}Ce^{j0}$ 、

$Z_{C}={\frac {e^{-j\pi /2}}{\omega C}}$ ，

或者，应用欧拉公式，

$Z_{C}={\frac {1}{j\omega C}}$ 。

电感器

通过电感器的含时电流 $i_{L}(t)$ 与电感器两端的含时电压 $v_{L}(t)$ ，两者之间的关系为

$v_{L}(t)=L{\frac {\operatorname {d} i_{L}(t)}{\operatorname {d} t}}$ 。

设定含时电流信号为

$i_{L}(t)=I_{0}\cos(\omega t)$ 。

则电压为

$v_{L}(t)=-\omega LI_{0}\sin(\omega t)=\omega LI_{0}\cos(\omega t+\pi /2)$ 。

两者的除商为

${\frac {v_{L}(t)}{i_{L}(t)}}={\frac {\omega L\cos(\omega t+\pi /2)}{\cos(\omega t)}}$ 。

所以，电感器阻抗的大小为 $\omega L$ ，交流电压超前90°于交流电流，或者，交流电流滞后90°于交流电压。

以相量形式表示，

$i_{L}(t)=I_{0}e^{j\omega t},\qquad I_{0}>0$ 、

$v_{L}(t)=\omega LI_{0}e^{j(\omega t+\pi /2)}$ 、

$Z_{L}=\omega Le^{j\pi /2}$ ，

或者，应用欧拉公式，

$Z_{L}=j\omega L$ 。

广义 s-平面阻抗

以 $j\omega$ 定义阻抗的方法只能应用于以稳定态交流信号为输入的电路。假若将阻抗概念加以延伸，将 $j\omega$ 改换为复角频率 $s$ ，就可以应用于以任意交流信号为输入的电路。表示于时域的信号，经过拉普拉斯变换后，会改为表示于频域的信号，改成以复角频率表示。采用这更广义的标记，基本电路元件的阻抗为

元件	阻抗表达式
电阻器	$R$
电容器	$1/sC$
电感器	$sL$

对于直流电路，这简化为 $s=0$ ；对于稳定正弦交流信号，$s=j\omega$ 。

电抗

主条目：电抗

电抗是阻抗的虚部。电阻 $R$ 与电抗 $X$ 共同设定阻抗的大小和相位：

$Z_{m}={\sqrt {ZZ^{*}}}={\sqrt {R^{2}+X^{2}}}$ 、

$\theta =\arctan {\left({\frac {X}{R}}\right)}$ 。

具有有限电抗的电路元件，会使得其两端的电压与通过的电流发生相位差 $\theta$ ：

$X=Z_{m}\sin \theta$ 。

运作时，纯电抗元件会交替地从电路吸收电能，然后又将电能还给电路；纯电抗元件不会耗散任何电能。

容抗

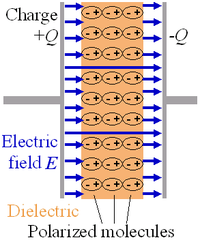
电介质分子因为电子受到电场影响，使得分子偏离平衡位置。为了方便说明，本图将电介质和电极的空隙加大，实际上电介质会直接和电极接触。

主条目：电容

理想电容器的阻抗是虚数，不具有实部，其虚部称为“容抗”，与信号的角频率成反比。电容器是由两块导体和夹在中间的电介质构成，其容抗为

$X_{C}=-j/\omega C$ 。

从这方程式可以观察到，当交流电源的角频率 $\omega$ 趋向于零时，电源会趋向于直流电源，容抗会趋向于负无穷大，假设给定电压源振幅，则电流会趋向于零。所以，在低频率运作时，电容器貌似断路。假设电源的频率越高，则容抗越低，对于电流通过的阻碍也越低。在高频率运作时，电容器貌似短路。

更详细地描述，假设连接直流电流源于平行板电容器的两端，由于电容器中有绝缘的电介质阻隔，电荷无法穿过电容器，电容器的一块平行板会累积正电荷,另一块平行板会累积负电荷。这过程称为“充电”。注意到在这充电过程，整个电容器仍旧维持电中性。分别累积于两块平行板的正电荷和负电荷会产生电场。依照不同的电介质属性而定，这电场会将电介质的正负电荷稍微分开，或者按照电场方向改变每一个电介质分子的定向，将电介质电极化，这会在电介质的表面形成面束缚电荷与其对应的感应电场，其方向与原本电场相反，因此减弱原本电场的实际作用，所以电介质可以增加电容器的电容。由于电容器的总电场，电容器的两块平行板之间会出现电压。等到这电压不再变动之后，通过电容器的电流会等于零，所以，一般会说电容器不允许直流电流通过。

假设连接交流电流源或交流电压源于平行板电容器的两端，由于电流会周期性的变换方向，交流电流会轮流对电容器的两块平行板充电和放电，处于两块平行板的电荷会周期性的变化，因此在一个周期内，除了电流由正变负（或由负变正）的那一瞬间之外，通过电容器的电流均不为零。因此，一般认为电容器可允许交流电流通过。注意到电容器只能够累积有限量的电荷。

感抗

主条目：电感

理想电感器的阻抗是虚数，不具有实部，其虚部称为“感抗”，与信号的角频率成正比：

$X_{L}=\omega Lj$ ；

其中，$X_{L}$ 是感抗。

从这方程式可以观察到，当交流电源的角频率趋向于零时，电源会趋向于直流电源，感抗会趋向于零，对于电流的通过阻碍越低。所以，在低频率运作时，电感器貌似短路。假设电源角频率越高，则感抗越高，假设给定电压源振幅，则电流会趋向于零。所以，在高频率运作时，电感器貌似断路。

电感器是一个线圈导体。根据法拉第感应定律，通过载流回圈的磁通量变率，会生成的感应电动势为

${\mathcal {E}}=-{{\operatorname {d} \Phi _{B}} \over \operatorname {d} t}$ ；

其中，${\mathcal {E}}$ 是感应电动势，$\Phi _{B}$ 是磁通量。

假设电感器的线圈匝数是 $N$ ，则感应电动势为

${\mathcal {E}}=-N{\operatorname {d} \Phi _{B} \over \operatorname {d} t}$ 。

感应电动势会阻碍电流流动。常定直流电所产生的磁场，其通过线圈的磁通量是个常数，变率为零，感应电动势也为零。所以，常定直流电会将电感器视为短路（通常电感器的材质为低电阻率材料）。交流电变率的时间平均值跟频率成正比，因此感抗与频率也成正比。

阻抗组合

主条目：串联电路和并联电路

应用串联电路和并联电路的阻抗计算定则，就可以计算出简单电路的总阻抗。除了阻抗是复数以外，这定则与串联电路和并联电路的电阻计算定则等同。但是，对于一般电路案例，还需要通过等效阻抗转换（equivalent impedance transform）这一道步骤。

星形电路和三角形电路示意图。

具有多于两个终端点的阻抗电路，无法约化为只具有一个阻抗元件的等效电路；具有 $n$ 个终端点的阻抗电路，$n>2$ ，最少只能约化为具有 $n$ 个阻抗元件的等效电路。三终端点电路可以约化为具有三个节点的三角形电路或具有四个节点的星形电路。这两种等价电路可以互相变换。具有任意个终端点的一般电路，只靠串联和并联组和，无法约化为具有最少个阻抗元件的电路（称为“最少电路”）；通常，还必需使用角星变换和星角变换。理论上，可以证明这些变换足够找到最少电路；不须要任何其他种复杂变换。

串联电路

以串联方式相连接的元件。

假设一个电路的元件是以串联方式相连接，则通过每一个元件的电流都相等，等效阻抗是每一个元件的阻抗的总和：

$Z_{eq}\ {\stackrel {def}{=}}\ Z_{1}+Z_{2}+\cdots +Z_{n}$ ；

其中，$Z_{eq}$ 是等效阻抗，$Z_{i}$ 是第 $i$ 个元件的阻抗。

以实部项目和虚部项目表示，

$Z_{eq}=R_{eq}+jX_{eq}=(R_{1}+R_{2}+\cdots +R_{n})+j(X_{1}+X_{2}+\cdots +X_{n})$ 。

并联电路

以并联方式相连接的元件。

假设一个电路的元件是以并联方式相连接，则每一个元件两端的电压都相等，每一个元件的阻抗的倒数，总和起来就是等效阻抗的倒数：

${\frac {1}{Z_{eq}}}\ {\stackrel {def}{=}}\ {\frac {1}{Z_{1}}}+{\frac {1}{Z_{2}}}+\cdots +{\frac {1}{Z_{n}}}$ 。

对于 $n=2$ 案例，

$Z_{eq}={\frac {Z_{1}Z_{2}}{Z_{1}+Z_{2}}}$ 。

以实部项目 $R_{eq}$ 和虚部项目 $X_{eq}$ 表示，

$Z_{eq}=R_{eq}+jX_{eq}$ ；

其中，

$R_{eq}={\frac {(X_{1}R_{2}+X_{2}R_{1})(X_{1}+X_{2})+(R_{1}R_{2}-X_{1}X_{2})(R_{1}+R_{2})}{(R_{1}+R_{2})^{2}+(X_{1}+X_{2})^{2}}}$ 、

$X_{eq}={\frac {(X_{1}R_{2}+X_{2}R_{1})(R_{1}+R_{2})-(R_{1}R_{2}-X_{1}X_{2})(X_{1}+X_{2})}{(R_{1}+R_{2})^{2}+(X_{1}+X_{2})^{2}}}$ 。

测量

当测量电路元件的阻抗时，必需先了解测量值与真实值之间可能会出现的差别。这是因为测量仪器本身的残馀阻抗和测量的准确度问题。给定已知阻抗真实值的元件，然后比较其测量值与真实值，就可以知道这测量方法的优劣。

测量阻抗的方法有很多种，例如，电桥法、谐振法、电压-电流法、阻抗频谱法等等。每一种方法都有其优点和缺点。测量者可以选择最适合的方法。

电桥法

交流电桥电路图

交流电桥貌似惠斯登桥，可以用来测量阻抗。将交流电源连接于交流电桥两端，电桥的四个元件的阻抗分别为 $Z_{1}$ ，$Z_{2}$ ，$Z_{3}$ ，$Z_{x}$ 。在BD两点之间的侦测器可以是耳机或交流检流器。当电桥达成平衡状态时，BD两点之间的电压为零，交流检流器测量出的电流也会为零，未知元件与另外三个元件之间关于阻抗的关系为

$Z_{x}=Z_{2}Z_{3}/Z_{1}$ ，

以相量表示，

$Z_{x}=|Z_{x}|\angle \theta _{x}=|Z_{2}Z_{3}/Z_{1}|\angle (\theta _{2}+\theta _{3}-\theta _{1})$ 。

这方法历史悠久，很容易制作成品仪器，费用低廉，准确率高；但是，不能够自动化，必需手工调整已知阻抗来达成平衡，而且电桥的测量频域比较狭窄。

谐振法

谐振法电路图

谐振法依赖RLC串联电路在共振状况的物理行为来测量元件的阻抗。这方法使用到品质因子（Q factor） $Q$ 的概念。一个RLC串联电路的品质因子是其共振频率与频宽的比率。这比率又可以证明为等于其电容器或电感器的电抗与电阻的比率。所以，使用测Q计（Q meter）测量一电路元件所得到的 $Q$ 值，等于这电路元件的电抗除以电路的电阻。

施加正弦电压源于电路。设定测试的频率为 $\omega$ 。阻抗测试分为两个步骤：

1. 调整可调电容器的电容 $C$ ，使得RLC电路进入共振状况。用测Q计测量电容器的品质因子 $Q$ 。
2. 如右图所示，将阻抗为 $Z_{x}$ 的被测元件串联于RLC电路，调整可调电容器的电容 $C'$ ，使得电路进入共振状况。用测Q计测量电容器的品质因子 $Q'$ 。

对于第一个共振状况，可调电容器的电抗 $X_{C}$ 与电感器的电抗 $X_{L}$ 之间的关系为

$X_{C}+X_{L}=0$ 。

所以，

${\frac {1}{\omega C}}=\omega L$ 。

从前面关于品质因子的论述，可以写出

$Q={\frac {|X_{C}|}{R}}={\frac {1}{\omega CR}}={\frac {\omega L}{R}}$ 。

对于第二个共振状况，被测元件的电抗 $X_{X}$ 为

$X_{C'}+X_{X}+X_{L}=0$ 。

所以，被测元件的电抗为

$X_{X}={\frac {1}{\omega C'}}-\omega L={\frac {1}{\omega C'}}-{\frac {1}{\omega C}}={\frac {C-C'}{\omega CC'}}$ ，

品质因子为

$Q'={\frac {|X_{C'}|}{R_{X}+R}}={\frac {1}{\omega C'(R_{X}+R)}}$ 。

所以，被测元件的电阻为

$R_{X}={\frac {1}{\omega C'Q'}}-{\frac {1}{\omega CQ}}$ 。

被测元件的阻抗为

$Z_{X}=R_{X}+jX_{X}=\left({\frac {1}{\omega C'Q'}}-{\frac {1}{\omega CQ}}\right)+j\left({\frac {1}{\omega C'}}-{\frac {1}{\omega C}}\right)$ 。

这方法可以用于测量高品质因子的元件。但是，必需手工调整来达成共振。

参阅

• 阻抗匹配
• 阻抗心动描记术（impedance cardiography）
• 阻抗电桥（impedance bridging）
• 特性阻抗（characteristic impedance）
• 负阻抗变换器（impedance bridging）

导抗
	实数	虚数	复数	单位
导性	电导（G）	电纳（B）	导纳（Y）	西门子（S）
抗性	电阻（R）	电抗（X）	阻抗（Z）	欧姆（Ω）

外部链接

• 乔治亚州州立大学（Georgia State University）线上物理网页：阻抗 （页面存档备份，存于互联网档案馆）
• Lewis Jr., George; George K. Lewis Sr. and William Olbricht. Cost-effective broad-band electrical impedance spectroscopy measurement circuit and signal analysis for piezo-materials and ultrasound transducers. Measurement Science and Technology. August 2008, 19 (10): 105102 [2008-09-15]. doi:10.1088/0957-0233/19/10/105102.