半导体
| 半导体器件制造 |
|---|
 |
| 金属氧化物半导体场效电晶体 |
|
未来
|
半导体（德语：Halbleiter, 英语：Semiconductor, 法语：Semi-conducteur），是一种电导率在绝缘体至导体之间的物质或材料。半导体在某个温度范围内，随温度升高而增加电荷载流子的浓度，使得电导率上升、电阻率下降；在绝对零度时，成为绝缘体。依有无加入掺杂剂，半导体可分为：本征半导体、杂质半导体（n型半导体、p型半导体）。
电导率容易受控制的半导体，可作为资讯处理的元件材料。从科技或是经济发展的角度来看，半导体非常重要。很多电子产品，如电脑、移动电话、数字录音机的核心单元都是利用半导体的电导率变化来处理资讯。常见的半导体材料有：第一代（另一种定义/说法：第一“类”）的硅、锗，第二代（类）的砷化镓、磷化铟，第三代（类）的氮化镓、氧化锌、氮化铝、碳化硅等；而硅更是各种半导体材料中，在商业应用上最具有影响力的一种。
材料的导电性是由导带中含有的电子数量决定。当电子从价带获得能量而跳跃至导电带时，电子就可以在带间任意移动而导电。一般常见的金属材料其导电带与价电带之间的能隙非常小，在室温下电子很容易获得能量而跳跃至导电带而导电，而绝缘材料则因为能隙很大（通常大于9电子伏特），电子很难跳跃至导电带，所以无法导电。
一般半导体材料的能隙约为1至3电子伏特，介于导体和绝缘体之间。因此只要给予适当条件的能量激发，或是改变其能隙之间距，此材料就能导电。
半导体通过电子传导或电洞传导的方式传输电流。电子传导的方式与铜线中电流的流动类似，即在电场作用下高度电离的原子将多余的电子向着负离子化程度比较低的方向传递。电洞导电则是指在正离子化的材料中，原子核外由于电子缺失形成的“空穴”，在电场作用下，空穴被少数的电子补入而造成空穴移动所形成的电流（一般称为正电流）。
材料中载流子（carrier）的数量对半导体的导电特性极为重要。这可以通过在半导体中有选择的加入其他“杂质”（IIIA、VA族元素）来控制。如果我们在纯矽中掺杂（doping）少许的砷或磷（最外层有5个电子），就会多出1个自由电子，这样就形成n型半导体；如果我们在纯矽中掺入少许的硼（最外层有3个电子），就反而少了1个电子，而形成一个电洞（hole），这样就形成p型半导体（少了1个带负电荷的原子，可视为多了1个正电荷）。
普通半导体如硅、砷化镓、碳化硅等材料中的电子和空穴通常可以用非相对论性的抛物线型色散关系来描述其能量-动能关系[1][2]，而在最近研发的新型半导体中，包括由麻省理工学院的唐爽和崔瑟豪斯夫人提出的准狄拉克材料、半狄拉克材料等（唐-崔瑟豪斯理论）[3][4][5]，电子和空穴可以具有不同的相对论效应。这些相对论性的新型半导体材料或可引领下一代计算机芯片、能源装置的研发。
概括
[编辑]
半导体和绝缘体之间的差异主要来自两者的能带宽度不同。绝缘体的能带比半导体宽，意即绝缘体价带中的载子必须获得比在半导体中更高的能量才能跳过能带，进入导带中。室温下的半导体导电性有如绝缘体，只有极少数的载子具有足够的能量进入导带。因此，对于一个在相同电场下的本征半导体和绝缘体会有类似的电特性，不过半导体的能带宽度小于绝缘体也意味著半导体的导电性更容易受到控制而改变。
纯质半导体的电气特性可以借由植入杂质的过程而永久改变，这个过程通常称为掺杂。依照掺杂所使用的杂质不同，掺杂后的半导体原子周围可能会多出一个电子或一个电洞，而让半导体材料的导电特性变得与原本不同。如果掺杂进入半导体的杂质浓度够高，半导体也可能会表现出如同金属导体般（类金属）的电性。在掺杂了不同极性杂质的半导体界面处会有一个内建电场（built-in electric field），内建电场和许多半导体元件的操作原理息息相关（例如太阳能电池电子与电洞对的搜集就是靠内建电场来作用），而掺杂后的半导体有许多电性也会有相对应的变化。
除了借由掺杂的过程永久改变电性外，半导体亦可因为施加于其上的电场改变而动态地变化。半导体材料也因为这样的特性，很适合用来作为电路元件，例如电晶体。电晶体属于主动式的（有源）半导体元件（active semiconductor devices），当主动元件和被动式的（无源）半导体元件（passive semiconductor devices）如电阻器或是电容器组合起来时，可以用来设计各式各样的集成电路产品，例如微处理器。
当电子从导带掉回价带时，减少的能量可能会以光的形式释放出来。这种过程是制造发光二极体以及半导体雷射的基础，在商业应用上都有举足轻重的地位。而相反地，半导体也可以吸收光子，透过光电效应而激发出在价带的电子，产生电讯号。这即是光探测器的来源，在光纤通讯或是太阳能电池的领域是最重要的元件，也是相机中CMOS Image Sensor主要的运作原理。
半导体有可能是单一元素组成，例如矽。也可以是两种或是多种元素的化合物，常见的化合物半导体有砷化镓或是磷化铝铟镓（aluminium gallium indium phosphide, AlGaInP）等。合金也是半导体材料的来源之一，如矽锗或是砷化镓铝（aluminium gallium arsenide, AlGaAs）等。
-
-
diamond structure（钻石结构） -
Zinkblende structure（闪锌结构）
电导率
[编辑]在常温下，半导体的电导率介于金属导体（～ S/m）和绝缘体（ < S/m）之间，一般为 ～ S/m [6]。
能带结构
[编辑]半导体中的电子所具有的能量被限制在基态与自由电子之间的几个能带里，在能带内部电子能量处于准连续状态，而能带之间则有带隙相隔开，电子不能处于带隙内。当电子在基态时，相当于此电子被束缚在原子核附近；而相反地，如果电子具备了自由电子所需要的能量，那么就能完全离开此材料。每个能带都有数个相对应的量子态，而这些量子态中，能量较低的都已经被电子所填满。这些已经被电子填满的量子态中，能量最高的就被称为价电带。半导体和绝缘体在正常情况下，几乎所有电子都在价电带或是其下的量子态里，因此没有自由电子可供导电。
半导体和绝缘体之间的差异在于两者之间能带间隙宽度不同，亦即电子欲从价带跳入导电带时所必须获得的最低能量不一样。通常能带间隙宽度小于3电子伏特（eV）者为半导体，以上为绝缘体。
在绝对零度时，固体材料中的所有电子都在价带中，而导电带为完全空置。当温度开始上升，高于绝对零度时，有些电子可能会获得能量而进入导电带中。导电带是所有能够让电子在获得外加电场的能量后，移动穿过晶体、形成电流的最低能带，所以导电带的位置就紧邻价电带之上，而导电带和价电带之间的差距即是能带间隙。通常对半导体而言，能带间隙的大小约为1电子伏特上下。在导电带中，和电流形成相关的电子通常称为自由电子。根据包利不相容原理，同一个量子态内不能有两个电子，所以绝对零度时，费米能级以下的能带包括价电带全部被填满。由于在填满的能带内，具有相反方向动量的电子数目相等，所以宏观上不能载流。在有限温度，由热激发产生的导电带电子和价电带电洞使得导电带和价电带都未被填满，因而在外电场下可以观测到宏观净电流。
在价电带内的电子获得能量后便可跃升到导电带，而这便会在价带内留下一个空缺，也就是所谓的电洞。导电带中的电子和价电带中的电洞都对电流传递有贡献，电洞本身不会移动，但是其它电子可以移动到这个电洞上面，等效于电洞本身往反方向移动。相对于带负电的电子，电洞的电性为正电。
由化学键结的观点来看，获得足够能量、进入导电带的电子也等于有足够能量可以打破电子与固体原子间的共价键，而变成自由电子，进而对电流传导做出贡献。
半导体和导体之间有个显著的不同是半导体的电流传导同时来自电子与电洞的贡献，而导体的费米能阶则已经在导带内，因此电子不需要很大的能量即可找到空缺的量子态供其跳跃、造成电流传导。
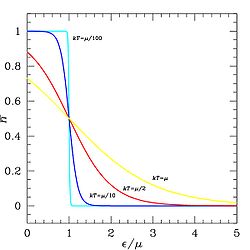
固体材料内的电子能量分布遵循费米-狄拉克分布。在绝对零度时，材料内电子的最高能量即为费米能阶，当温度高于绝对零度时，费米能阶为所有能阶中，被电子占据机率等于0.5的能阶。半导体材料内电子能量分布为温度的函数也使其导电特性受到温度很大的影响，当温度很低时，可以跳到导电带的电子较少，因此导电性也会变得较差。
能量-动量色散
[编辑]上述关于能带结构的内容为了简化，因此跳过了一个重要的现象，称为能量的色散（dispersion of energy）。同一个能带内之所以会有不同能量的量子态，原因是能带的电子具有不同波向量或者“k-向量”。在[学]]中，k-向量即为粒子的动量，不同的材料会有不同的能量-动量关系（E-k relationship）。
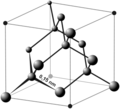
能量-动量色散关系式能决定电子或电洞的等效质量（effective mass），以代表，公式如下：
![{\displaystyle m^{*}=\hbar ^{2}\cdot \left[{{d^{2}E(k)} \over {dk^{2}}}\right]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0927dd417fe1e3d16db826583173c6e454fb30de)
等效质量可视为联系量子力学与古典力学的一个参数。这个参数对于半导体材料而言十分重要，例如它和电子或电洞的迁移率（electrons or holes mobility）有高度关联。电子或电洞的迁移率对于半导体元件的载子传输是相当基本的参数。
电子和电洞的等效质量不相等，这也造成了两者的迁移率不同，进而让“N-通道”和“P-通道”的金属氧化物半导体场效电晶体导电性不同。
准确的说应该是动量变化为零，因为任何时候动量都是守恒的，不能说不必牵涉
半导体材料的导电带底部和价电带顶端在“能量-动量座标”上可能会处在不同的k值，这种材料叫做间接能带材料（in-direct bandgap material），例如矽或是锗。相对地，如果某种材料的导带底部和价带顶端有相同的k值，这种材料称为直接能带材料（direct bandgap material），最常见的例子是砷化镓。电子在直接能隙材料的价带与导带的跃迁不涉及晶格动量的改变，因此发光的效率高过间接能隙材料甚多，砷化镓也因此是光电半导体元件中最常见的材料之一。
载流子的产生与复合
[编辑]当离子化的辐射能量落在半导体时，可能会让价带中的电子吸收到足够能量而跃迁至导带，并在价带中产生一个电洞，这种过程叫做电子-电洞对的产生（generation of electron-hole pair）[7]。而其他够大的能量，如热能，也可以同样产生出电子-电洞对。
电子-电洞对则会经由复合的过程而被消灭。根据能量守恒的观念，在导带中的电子必须回到价带，将所得到的能量释放出来。能量释放的形式包括热能或辐射能，而这两种能量量子化后的表征分别是声子以及光子。
对于处在稳态的半导体而言，电子-电洞对的产生与复合速率是相等的。而在一个已给定的温度下，电子-电洞对的数量可由量子统计求得。量子力学处理此类问题时必须同时遵守能量以及动量守恒。
掺杂
[编辑]半导体之所以能广泛应用在今日的数位世界中，凭借的就是其能借由在本质半导体加入杂质改变其特性，这个过程称之为掺杂。掺杂进入本质半导体的杂质浓度与极性皆会对半导体的导电特性产生很大的影响。而掺杂过的半导体则称为杂质半导体。
掺杂物
[编辑]哪种材料适合作为某种半导体材料的掺杂物需视两者的原子特性而定。一般而言，掺杂物依照其带给被掺杂材料的电荷正负被区分为施体（donor）与受体。施体原子带来的价电子多会与被掺杂的材料原子产生共价键，进而被束缚。而没有和被掺杂材料原子产生共价键的电子则会被施体原子微弱地束缚住，这个电子又称为施体电子。和本征半导体的价电子比起来，施体电子跃迁至导带所需的能量较低，比较容易在半导体材料的晶格中移动，产生电流。虽然施体电子获得能量会跃迁至导带，但并不会和本征半导体一样留下一个电洞，施体原子在失去了电子后只会固定在半导体材料的晶格中。因此这种因为掺杂而获得多馀电子提供传导的半导体称为n型半导体，n代表带负电荷的电子。
和施体相对的，受体原子进入半导体晶格后，因为其价电子数目比半导体原子的价电子数量少，等效上会带来一个的空位，这个多出的空位即可视为电洞。受体掺杂后的半导体称为p型半导体，p代表带正电荷的电洞。
以一个矽的本征半导体来说明掺杂的影响。矽有四个价电子，常用于矽的掺杂物有三价与五价的元素。当只有三个价电子的三价元素如硼掺杂至矽半导体中时，硼扮演的即是受体的角色，掺杂了硼的矽半导体就是p型半导体。反过来说，如果五价元素如磷掺杂至矽半导体时，磷扮演施体的角色，掺杂磷的矽半导体成为n型半导体。
一个半导体材料有可能先后掺杂施体与受体，而如何决定此外质半导体为n型或p型必须视掺杂后的半导体中，受体带来的电洞浓度较高或是施体带来的电子浓度较高，亦即何者为此外质半导体的多数载流子（majority carrier）。和多数载流子相对的是少数载流子（minority carrier）。对于半导体元件的工作原理分析而言，少数载流子在半导体中的行为有著非常重要的地位。
材料的制造
[编辑]
为了满足量产上的需求，半导体的电性必须是可预测并且稳定的，因此包括掺杂物的纯度以及半导体晶格结构的品质都必须严格要求。常见的品质问题包括晶格的位错（dislocation）、孪晶面（twins）或是堆垛层错（stacking fault）[8] 都会影响半导体材料的特性。对于一个半导体元件而言，材料晶格的缺陷（晶体缺陷）通常是影响元件性能的主因。
目前用来成长高纯度单晶半导体材料最常见的方法称为柴可拉斯基制程（钢铁场常见工法）。这种制程将一个单晶的晶种（seed）放入溶解的同材质液体中，再以旋转的方式缓缓向上拉起。在晶种被拉起时，溶质将会沿著固体和液体的介面固化，而旋转则可让溶质的温度均匀。
全球制造企业
[编辑]| 排序 | 公司 | 生产模式 | 国家 | 2012年营收（百万美金） | 2011年营收（百万美金） | 较2011年成长 |
|---|---|---|---|---|---|---|
| 1 | 英特尔 | IDM |  美国
|
49114 | 49697 | -1% |
| 2 | 三星半导体 | IDM |  韩国
|
32251 | 33483 | -4% |
| 3 | 台积电 | 晶圆代工 |  中华民国
|
17167 | 14600 | 18% |
| 4 | 高通 | IC设计 | 美国
|
13177 | 9828 | 34% |
| 5 | 德州仪器 | IDM | 美国
|
12147 | 12182 | -6% |
| 6 | 东芝 | IDM |  日本
|
11217 | 12745 | -12% |
| 7 | 瑞萨电子 | IDM | 日本
|
9314 | 10653 | -13% |
| 8 | 海力士 | IDM | 韩国
|
9057 | 9403 | -4% |
| 9 | 意法半导体 | IDM |  法国 义大利
|
8364 | 9631 | -13% |
| 10 | 美光 | IDM | 美国
|
8002 | 8571 | -7% |
| 11 | 博通 | IC设计 | 美国
|
7793 | 7160 | 9% |
| 12 | 索尼 | IDM | 日本
|
5709 | 6093 | -6% |
| 13 | 超微半导体 | IC设计 | 美国
|
5422 | 6568 | -17% |
| 14 | 英飞凌 | IDM |  德国
|
4993 | 5599 | -11% |
| 15 | 格罗方德 | 晶圆代工 | 美国
|
4560 | 3480 | 31% |
| 16 | 辉达 | IC设计 | 美国
|
4229 | 3939 | 7% |
| 17 | 富士通 | IDM | 日本
|
4162 | 4430 | -6% |
| 18 | 恩智浦半导体 | IDM |  荷兰
|
4157 | 4147 | 0% |
| 19 | 飞思卡尔 | IDM | 美国
|
3735 | 3164 | -15% |
| 20 | 联华电子 | 晶圆代工 | 中华民国
|
3730 | 3760 | -1% |
| 21 | 联发科技 | IC设计 | 中华民国
|
3366 | 2969 | 13% |
| 22 | 夏普 | IDM | 日本
|
3304 | 2908 | 14% |
| 23 | 美满电子 | IDM | 美国
|
3157 | 3445 | -8% |
| 24 | 尔必达* | IDM | 日本
|
3735 | 3164 | -15% |
| 25 | 罗姆电子 | IDM | 日本
|
3030 | 3303 | -8% |
- 尔必达于2012年5月宣告破产，2013年7月由美光完成并购。
十大公司
[编辑]| 公司 | 收入 | 净收入 | 市值 | 一年追踪回报率 | 交易所 |
|---|---|---|---|---|---|
| 美国英特尔公司（INTC） |
757亿美元 | 227亿美元 | 2561亿美元 | 34.1％ | 纳斯达克 |
| 中华民国台积电（TSM） |
379亿美元 | 131亿美元 | 2935亿美元 | 58.8％ | 纽约证券交易所 |
| 美国高通公司（QCOM） |
247亿美元 | 40亿美元 | 1,012亿美元 | 34.2％ | 纳斯达克 |
| 美国Broadcom Inc.（AVGO） |
229亿美元 | 25亿美元 | 1261亿美元 | 23.4％ | 纳斯达克 |
| 美国美光科技公司（MU） |
196亿美元 | 23亿美元 | 567亿美元 | 57.1％ | 纳斯达克 |
| 美国德州仪器（TXN） |
141亿美元 | 50亿美元 | 1158亿美元 | 21.8％ | 纳斯达克 |
| 中华民国日月光半导体有限公司（ASX） |
137亿美元 | 6亿美元 | 97亿美元 | 30.9％ | 纽约证券交易所 |
| 美国NVIDIA Corp.（NVDA） |
118亿美元 | 33亿美元 | 2272亿美元 | 155.5％ | 纳斯达克 |
| 意法半导体（STM） |
97亿美元 | 9亿美元 | 239亿美元 | 74.5％ | 纽约证券交易所 |
| 恩智浦半导体NV（NXPI） |
88亿美元 | 2亿美元 | 326亿美元 | 32.0％ | 纳斯达克 |
截止到2020年6月，根据TTM对全球半导体公司收入的追踪，整理出全球十大半导体公司（此列表仅限于直接或者通过美国或加拿大公开交易的公司，一般外国的公司会每半年提交报告一词，因此滞后时间会更长，所有数据截止2020年6月18日，所有数据由YCharts提供10 Biggest Semiconductor Companies（页面存档备份，存于互联网档案馆）
应用
[编辑]半导体器件可以通过结构和材料上的设计达到控制电流传输的目的，并以此为基础构建各种处理不同信号的电路。这是半导体在当前电子技术中广泛应用的原因。
延伸阅读
[编辑]工业
[编辑]参考来源
[编辑]- 文献
- Muller, Richard S.; Theodore I. Kamins. Device Electronics for Integrated Circuits 2d. New York: Wiley. 1986. ISBN 978-0-471-88758-4.
- Sze, Simon M. Physics of Semiconductor Devices（2nd ed.）. John Wiley and Sons（WIE）. 1981. ISBN 978-0-471-05661-4.
- 上册：施敏; 伍国珏; 译者：张鼎张、刘柏村. 半導體元件物理學(上冊). 台湾: 国立交通大学. 2008-08-01 [2008]. ISBN 978-986-843-951-1 （中文）. （繁体中文）
- 下册：施敏; 伍国珏; 译者：张鼎张、刘柏村. 半導體元件物理學(下冊). 台湾: 国立交通大学. 2009-04-14 [2009]. ISBN 978-986-843-954-2 （中文）. （繁体中文）
- Turley, Jim. The Essential Guide to Semiconductors. Prentice Hall PTR. 2002. ISBN 978-0-13-046404-0.
- Paul, Steffen; Paul, Reinhold. Grundlagen der Elektrotechnik und Elektronik 1: Gleichstromnetzwerke und ihre Anwendungen. Springer Vieweg. 2023. ISBN 978-3-662-66187-1.
- Yu, Peter Y.; Cardona, Manuel. Fundamentals of Semiconductors : Physics and Materials Properties. Springer. 2004. ISBN 978-3-540-41323-3.
- Neamen, Donald A. Semiconductor Physics and Devices: Basic Principles (3rd ed.). McGraw-Hill Higher Education. 2003. ISBN 0-07-232107-5.
- 引用
- ^ Charles Kittel. op. cit. 1996: 202. ISBN 978-0-471-11181-8.
- ^ Green, M. A. Intrinsic concentration, effective densities of states, and effective mass in silicon. Journal of Applied Physics. 1990, 67 (6): 2944–2954. Bibcode:1990JAP....67.2944G. doi:10.1063/1.345414.
- ^ New material shares many of graphene’s unusual properties. Thin films of bismuth-antimony have potential for new semiconductor chips, thermoelectric devices （页面存档备份，存于互联网档案馆）. MIT News Office (24 April 2012).
- ^ Tang, Shuang; Dresselhaus, Mildred. Constructing Anisotropic Single-Dirac-Cones in BiSb Thin Films. Nano Letters. 2012, 12 (4): 2021–2026. doi:10.1021/nl300064d.
- ^ Tang, Shuang; Dresselhaus, Mildred. Constructing A Large Variety of Dirac-Cone Materials in the BiSb Thin Film System. Nanoscale. 2012, 4 (24): 7786–7790. doi:10.1039/C2NR32436A.
- ^ 存档副本. [2022-04-15]. （原始内容存档于2022-04-15）.
- ^ 由萨支唐教授提出
- ^ J. P. Hirth and J. Lothe (1992). Theory of dislocations (2 ed.). Krieger Pub Co. ISBN 978-0-89464-617-1.
- ^ Top Semiconductor Ranking 2012. [2013-12-28]. （原始内容存档于2013-12-30）.
相关条目
[编辑]外部链接
[编辑]- Howstuffworks' semiconductor page（页面存档备份，存于互联网档案馆）
- US Navy Electrical Engineering Training Series
- NSM-Archive（页面存档备份，存于互联网档案馆） Physical Properties of Semiconductors
- Semiconductor Concepts at Hyperphysics（页面存档备份，存于互联网档案馆）
- Principles of Semiconductor Devices（页面存档备份，存于互联网档案馆） by Bart Van Zeghbroeck, University of Colorado
- Semiconductor OneSource Hall of Fame（页面存档备份，存于互联网档案馆）、Glossary
- SiliconFarEast.com（页面存档备份，存于互联网档案馆） What is a semiconductor?
