数学上,克利福德代数(Clifford algebra)是由具有二次型的向量空间生成的单位结合代数。作为域上的代数,其推广实数系、复数系、四元数系等超复数系,以及外代数。[1][2]此代数结构得名自英国数学家威廉·金顿·克利福德。
研究克里福代数的理论有时也称为克里福代数,其与二次型论和正交群理论紧密联系。其在几何、理论物理、数码图像处理中有很多应用。其主要贡献者有:威廉·哈密顿(四元数),赫尔曼·格拉斯曼(外代数),威廉·金顿·克利福德,David Hestenes等。
最常见的克里福代数是正交克里福代数,又称(伪)黎曼克里福代数。另一类是扭对称克里福代数。[3]
设有域 上的向量空间
上的向量空间 ,且其上有二次型
,且其上有二次型 。克里福代数
。克里福代数 是由
是由 生成的“最自由”的单位结合代数,但须满足[a]
生成的“最自由”的单位结合代数,但须满足[a]

其中左边的平方是该代数中的乘法,而右边的 为其乘法单位元。所谓“最自由”,可以用泛性质严格定义,详见下节。
为其乘法单位元。所谓“最自由”,可以用泛性质严格定义,详见下节。
若 为有限维实向量空间,且
为有限维实向量空间,且 非退化,则
非退化,则 可记为
可记为 ,表示
,表示 有一组正交基,其中
有一组正交基,其中 个基元
个基元 满足
满足 ,另有
,另有 个基元满足
个基元满足 ,而
,而 指明该克里福代数定义在实域上,即该代数的元素系数皆为实数。此组正交基可藉正交对角化找出。
指明该克里福代数定义在实域上,即该代数的元素系数皆为实数。此组正交基可藉正交对角化找出。
由 生成的自由代数是张量代数
生成的自由代数是张量代数 。换言之,其为
。换言之,其为 自身的
自身的 重张量积,对所有
重张量积,对所有 的直和。故相应的克里福代数会是该张量代数对元素
的直和。故相应的克里福代数会是该张量代数对元素 (
( 取遍
取遍 的元素)生成的双边理想的商。张量积导出在商代数的乘积以串接表示(例如
的元素)生成的双边理想的商。张量积导出在商代数的乘积以串接表示(例如 )。其结合律由张量积的结合律推出。
)。其结合律由张量积的结合律推出。
克里福代数有指明的子空间 ,即嵌入的像。若只得与克里福代数同构的
,即嵌入的像。若只得与克里福代数同构的 代数,则一般无法唯一确定该子空间。
代数,则一般无法唯一确定该子空间。
若底域 的特征不为
的特征不为 ,则可将基本恒等式
,则可将基本恒等式 重写成
重写成

其中

定义的对称双线性形式与二次型 之间有极化恒等式。
之间有极化恒等式。
特征为 的二次型与克里福代数为特例。具体而言,若
的二次型与克里福代数为特例。具体而言,若 ,则对于二次型
,则对于二次型 ,式
,式 未必唯一确定某个对称双线性型
未必唯一确定某个对称双线性型 ,
, 也未必有正交基。本条目不少命题的条件皆要求特征不为
也未必有正交基。本条目不少命题的条件皆要求特征不为 ,而若允许特征为
,而若允许特征为 ,则命题不再成立。
,则命题不再成立。
克里福代数与外代数密切相关。外代数是克里福代数的特例:若在克里福代数的定义中,取 ,则克里福代数
,则克里福代数 就是外代数
就是外代数 。即使
。即使 非零,只要基域
非零,只要基域 的特征非
的特征非 ,
, 和
和 之间仍有典范的线性同构。换言之,两者作为向量空间自然地同构,但其上的乘法有分别。特征为
之间仍有典范的线性同构。换言之,两者作为向量空间自然地同构,但其上的乘法有分别。特征为 时,两者仍线性同构,然而该同构并非自然。克里福代数的乘法和指定的子空间是比外代数更丰富的结构,因为用到
时,两者仍线性同构,然而该同构并非自然。克里福代数的乘法和指定的子空间是比外代数更丰富的结构,因为用到 提供的额外资讯。
提供的额外资讯。
克里福代数为滤套代数,而相伴的分次代数为外代数。
具体而言,克里福代数可视为外代数的“量子化”(见量子群),正如外尔代数为对称代数的量子化。
外尔代数和克里福代数还具有*-代数的结构,并能整合成某个超代数的偶次和奇次项,见典范对易与反对易关系代数。
设 为域
为域 上的向量空间,
上的向量空间, 为
为 上的二次型。多数情况下,域
上的二次型。多数情况下,域 是实域
是实域 或复域
或复域 ,或有限域
,或有限域 。
。
克里福代数 定义为有序对
定义为有序对 ,[b][5]其中
,[b][5]其中 为
为 上的单位结合代数,而线性映射
上的单位结合代数,而线性映射 满足对任意
满足对任意 ,皆有
,皆有 ,且
,且 满足下列泛性质:给定
满足下列泛性质:给定 上任何单位结合代数
上任何单位结合代数 和线性映射
和线性映射 令
令

(其中 表示
表示 的乘法单位元),必有唯一的代数同态
的乘法单位元),必有唯一的代数同态 使得以下图表可交换(即
使得以下图表可交换(即 :
:
二次型 可换成满足
可换成满足 的(无需对称的)双线性形式
的(无需对称的)双线性形式 ,此时
,此时 需满足的条件等价于
需满足的条件等价于

当基域的特征非 时,以上条件也等价于:
时,以上条件也等价于:

其中双线性型不妨限定为对称双线性型。
以上描述的克里福代数必定存在,能藉以下一般方法构造:先选取由 生成的最自由的代数,即张量代数
生成的最自由的代数,即张量代数 ,然后藉取商,保证基本恒等式成立。对于克里福代数,所需
,然后藉取商,保证基本恒等式成立。对于克里福代数,所需 的双边理想
的双边理想 是由所有形如
是由所有形如

的元素生成,其中 取遍
取遍 的元素,随后便可定义
的元素,随后便可定义 为商代数
为商代数 。
。
商承继的环乘积有时称为克里福积[6]:8–9,以免与外代数的外积 或纯量积
或纯量积 混淆。
混淆。
有上述 的构造后,可以直接验证
的构造后,可以直接验证 包含
包含 ,且满足所需的泛性质。而由泛性质,可知
,且满足所需的泛性质。而由泛性质,可知 在唯一同构的意义下唯一,故在此意义下,可当克里福代数必定由上述构造给出。从构造可知,
在唯一同构的意义下唯一,故在此意义下,可当克里福代数必定由上述构造给出。从构造可知, 是单射,故通常隐藏
是单射,故通常隐藏 而视
而视 为
为 的线性子空间。
的线性子空间。
因为克里福代数可由泛性质定义,所以 的构造具函子性,即
的构造具函子性,即 为函子,其定义域为具有二次型的
为函子,其定义域为具有二次型的 -向量空间组成的范畴(其态射为保二次型的线性映射),陪域为结合
-向量空间组成的范畴(其态射为保二次型的线性映射),陪域为结合 -代数范畴。泛性质保证,向量空间之间保二次型的线性映射,唯一扩展成相应的克里福代数的代数同态。
-代数范畴。泛性质保证,向量空间之间保二次型的线性映射,唯一扩展成相应的克里福代数的代数同态。
由于 已配备二次型
已配备二次型 ,在特征非
,在特征非 时,
时, 有一组正交基,即其元素
有一组正交基,即其元素 满足
满足
 ,及
,及 。
。
基本克里福恒等式推出,对于正交基,有
 ,及
,及 。
。
此关系使正交基元间的运算很容易。给定 中两两互异的正交基元的乘积
中两两互异的正交基元的乘积 ,可以将各因子按顺序排好,而仅需依照置换的奇偶性在前面加上正负号。
,可以将各因子按顺序排好,而仅需依照置换的奇偶性在前面加上正负号。
若 在
在 上的维数为
上的维数为 ,且
,且 为
为 的正交基,则
的正交基,则 为
为 上的向量空间,其一组基为
上的向量空间,其一组基为
 .
.
在上式中,空乘积( )定义为乘法单位元。由于每个
)定义为乘法单位元。由于每个 可以出现或不出现在乘积中,
可以出现或不出现在乘积中, 的维数(即基的大小)为
的维数(即基的大小)为

克里福代数的重要例子源自实或复向量空间及其上非退化的二次型给出。
本节的例子 和
和 皆同构于某个
皆同构于某个 或
或 ,其中
,其中 为
为 、
、 或
或 上的全个矩阵环。此类代数的完整分类,见克里福代数的分类。
上的全个矩阵环。此类代数的完整分类,见克里福代数的分类。
克里福代数有时称为几何代数,尤其定义在实域上时。
有限维实向量空间上的非退化二次型必等价于某个标准对角型:

其中 为向量空间的维数。非负整数对
为向量空间的维数。非负整数对 称为二次型的符号。配备此二次型的实向量空间一般记为
称为二次型的符号。配备此二次型的实向量空间一般记为 ,而
,而 生成的克里福代数则记为
生成的克里福代数则记为 。
。 可能表示
可能表示 或
或 ,视乎作者偏好二次型正定抑或负定。
,视乎作者偏好二次型正定抑或负定。
 的标准基
的标准基 由
由 支两两正交的向量组成,其中
支两两正交的向量组成,其中 支的平方为
支的平方为 ,其馀
,其馀 支的平方则为
支的平方则为 。于是,代数
。于是,代数 中,也有该
中,也有该 支向量的平方为
支向量的平方为 ,该
,该 支向量的平方为
支向量的平方为 。
。
低维的例子有:
 与
与 自然同构,因为并无非零向量。
自然同构,因为并无非零向量。 为由
为由 (其平方为
(其平方为 )生成的二维代数,从而与复数域
)生成的二维代数,从而与复数域 代数同构。
代数同构。 为由
为由 张成的四维代数。后三个基元的平方皆为
张成的四维代数。后三个基元的平方皆为 ,且两两相反交换,故代数与四元数系
,且两两相反交换,故代数与四元数系 同构。
同构。 为八维代数,与直和
为八维代数,与直和 (分裂复四元数系)同构。
(分裂复四元数系)同构。
也可以研究复域上的克里福代数。 维复向量空间上,每个非退化二次型都等价于标准对角型
维复向量空间上,每个非退化二次型都等价于标准对角型

由此,对每个维数 ,在同构意义下,恰有一个克里福代数定义在配备非退化二次型的
,在同构意义下,恰有一个克里福代数定义在配备非退化二次型的 维复向量空间上,记为
维复向量空间上,记为 。
。
最小的几个例子为:
 ,复数系,
,复数系, ,双复数系,
,双复数系, ,复四元数系,其中
,复四元数系,其中 表示复域上的
表示复域上的 矩阵组成的代数。
矩阵组成的代数。
本节将会构造哈密顿的四元数系,作为克里福代数 的偶子代数。
的偶子代数。
设 为实三维向量空间
为实三维向量空间 ,二次型
,二次型 为欧氏度量的相反数,则对于
为欧氏度量的相反数,则对于 ,相应的纯量积(双线性型)由
,相应的纯量积(双线性型)由

给出。
现引入向量 的克里福积
的克里福积 ,使其满足
,使其满足

(此处有负号,以使该代数与四元数的联系更清晰。)
设 为
为 的一组正交单位基,则由上式可知,其两两的克里福积满足
的一组正交单位基,则由上式可知,其两两的克里福积满足

且

克里福代数 的任意元素可以表示成
的任意元素可以表示成

若只考虑偶次项,则得到偶子代数![{\displaystyle \mathrm {Cl} _{0,3}^{[0]}(\mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6541725197b4f192001bd32ca1cf8b678d576da5) ,其任意元素可表示成
,其任意元素可表示成

若定义四元数的基元 为
为

则可知![{\displaystyle \mathrm {Cl} _{0,3}^{[0]}(\mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6541725197b4f192001bd32ca1cf8b678d576da5) 与哈密顿的实四元数代数同构,理由是:
与哈密顿的实四元数代数同构,理由是:


且

与四元数的运算法则一致。
本节构造二元四元数系,作为配备退化二次型的实四维向量空间的偶克里福代数。[7][8]
设向量空间 为实四维空间
为实四维空间 ,并设二次型
,并设二次型 为源自
为源自 上欧氏度量的退化型,即相应的双线性型
上欧氏度量的退化型,即相应的双线性型 满足:对任意
满足:对任意 ,
,

换言之,此退化纯量积只考虑将 投影到
投影到 后的像。
后的像。
向量 的克里福积
的克里福积 由下式定义:
由下式定义:

同上节,负号是为了明确该代数与四元数系的对应关系。
记 的标准基元为
的标准基元为 ,则其克里福积满足关系
,则其克里福积满足关系

及

克里福代数 也记为
也记为 (下标分别表示平方为
(下标分别表示平方为 的基元个数),其一般元素有16项,而仅取偶次项时,得到偶子代数
的基元个数),其一般元素有16项,而仅取偶次项时,得到偶子代数![{\displaystyle \mathrm {Cl} ^{[0]}(\mathbb {R} ^{4},d)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99eff326ee15b18fc9a58606715d26fb85642933) ,其一般元素形如
,其一般元素形如

于是,可分别定义四元数基元 和二元数基元
和二元数基元 为
为

从而给出 与二元四元数代数的同构。
与二元四元数代数的同构。
要验证二元四元数的乘法法则,可以计算

和

后者的计算中, 和
和 的换位将符号改变了偶数次(即无改变)。同样的方法能证明,二元数基元
的换位将符号改变了偶数次(即无改变)。同样的方法能证明,二元数基元 可与全部四元数基元
可与全部四元数基元 交换。
交换。
设 为特征非
为特征非 的域。
的域。
对于 的情况,若
的情况,若 有对角化
有对角化 ,即存在非零向量
,即存在非零向量 令
令 ,则
,则 代数同构于
代数同构于![{\displaystyle K[x]/(x^{2}-a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c62c3e9a4da297f0a0758ff5849fbfe553242cc) ,即由满足
,即由满足 的单一个元素
的单一个元素 生成的
生成的 -代数。
-代数。
更具体而言,有三种情况:
- 若
 (即
(即 为零二次型),则
为零二次型),则 代数同构于
代数同构于 上的二元数代数。
上的二元数代数。
- 若
 非零,且为
非零,且为 中的平方数,则
中的平方数,则 。
。
- 其馀情况下,
 同构于
同构于 的二次域扩张
的二次域扩张 。
。
对于 的情况,若
的情况,若 有对角化
有对角化 ,其中
,其中 皆非零(
皆非零( 非退化时必然存在),则
非退化时必然存在),则 同构于由
同构于由 生成的
生成的 -代数,其中
-代数,其中 满足
满足 。
。
于是 同构于(广义)四元数代数
同构于(广义)四元数代数 。在
。在 且
且 时,该代数化归为哈密顿的四元数代数,即
时,该代数化归为哈密顿的四元数代数,即 。
。
作为特殊情况,若有某个 使得
使得 ,则
,则 是二阶方阵的代数。
是二阶方阵的代数。
给定向量空间 ,可以构造外代数
,可以构造外代数 ,其定义不取决于
,其定义不取决于 上任何二次型。事实上,若
上任何二次型。事实上,若 的特征非
的特征非 ,则
,则 与
与 作为向量空间自然同构(而在特征
作为向量空间自然同构(而在特征 时,仍有同构,但不一定自然)。该自然同构当且仅当
时,仍有同构,但不一定自然)。该自然同构当且仅当 时为代数同构。所以,可以将克里福代数
时为代数同构。所以,可以将克里福代数 视为
视为 的外代数额外配备取决于
的外代数额外配备取决于 的乘法。(准确而言是外代数的“量子化”,见#作为外代数的量子化。)原有的外积仍有不取决于
的乘法。(准确而言是外代数的“量子化”,见#作为外代数的量子化。)原有的外积仍有不取决于 的定义。
的定义。
描述以上同构的简单方法是:先取 的正交基
的正交基 ,并扩展成
,并扩展成 的基(如#基与维数所述)。定义映射
的基(如#基与维数所述)。定义映射 使
使

并线性扩展。注意此处用到 正交。可以证明,映射
正交。可以证明,映射 的定义无关正交基的选择,故为自然同构。
的定义无关正交基的选择,故为自然同构。
若 的特征为
的特征为 ,则也可以藉反对称化(antisymmetrizing)定义以上同构:定义一列映射
,则也可以藉反对称化(antisymmetrizing)定义以上同构:定义一列映射 使
使

其求和符号中, 取遍
取遍 阶对称群
阶对称群 的元素。由于
的元素。由于 反对称,其导出独一个映射
反对称,其导出独一个映射 。该些映射的直和为
。该些映射的直和为 至
至 的线性映射。可以证明该映射为同构,且是自然同构。
的线性映射。可以证明该映射为同构,且是自然同构。
也可以从更高等的观点,在 上构造滤过,以看待两者的关系。注意张量代数
上构造滤过,以看待两者的关系。注意张量代数 有自然滤过
有自然滤过 ,其中
,其中 含所有阶不高于
含所有阶不高于 的张量。将此滤过投射到克里福代数上,就得到
的张量。将此滤过投射到克里福代数上,就得到 上的滤过。与此滤过相伴的分次代数
上的滤过。与此滤过相伴的分次代数

与外代数 自然同构。由于滤过代数的相伴分次代数总与原滤过代数作为滤过向量空间同构(藉选取
自然同构。由于滤过代数的相伴分次代数总与原滤过代数作为滤过向量空间同构(藉选取 在
在 中的补集),可知克里福代数与外代数在任何特征(包括
中的补集),可知克里福代数与外代数在任何特征(包括 )下皆同构(尽管不一定自然)。
)下皆同构(尽管不一定自然)。
本节假设特征非 。[c]
。[c]
克里福代数为 -分次代数(又称为超代数),以下说明原因。在
-分次代数(又称为超代数),以下说明原因。在 上,线性映射
上,线性映射 (关于原点对称)保持二次型
(关于原点对称)保持二次型 ,故由克里福代数的泛性质,该线性映射延拓成代数自同构
,故由克里福代数的泛性质,该线性映射延拓成代数自同构

由于 为对合(即其平方为恒同映射),可以将
为对合(即其平方为恒同映射),可以将 分解成
分解成 的正和负特征空间:
的正和负特征空间:
![{\displaystyle \operatorname {Cl} (V,Q)=\operatorname {Cl} ^{[0]}(V,Q)\oplus \operatorname {Cl} ^{[1]}(V,Q),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f839fb22e8ff47a3cd64ae06d9a6338584ff0a5)
其中
![{\displaystyle \operatorname {Cl} ^{[i]}(V,Q)=\left\{x\in \operatorname {Cl} (V,Q)\mid \alpha (x)=(-1)^{i}x\right\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6902ed1e7c0361df4271000a56e7b76c029990e)
由于 是自同构,有:
是自同构,有:
![{\displaystyle \operatorname {Cl} ^{[i]}(V,Q)\operatorname {Cl} ^{[j]}(V,Q)=\operatorname {Cl} ^{[i+j]}(V,Q),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25f34257a1d5cb5d629f65bf4806f4644ce0fb33)
其中方括号上标的运算模 ,故上式赋予
,故上式赋予 作为
作为 -分次代数的结构。子空间
-分次代数的结构。子空间![{\displaystyle \mathrm {Cl} ^{[0]}(V,Q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b95e0638819f9c71415acd8045a5b8df5eda754) 为
为 的子代数,称为偶子代数。而子空间
的子代数,称为偶子代数。而子空间![{\displaystyle \mathrm {Cl} ^{[1]}(V,Q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f04cddd1b4026240bc7face04ef5d2c4f25639a) 则称为奇部(其不为子代数)。此
则称为奇部(其不为子代数)。此 -分次在克里福代数的分析和应用上很重要。自同构
-分次在克里福代数的分析和应用上很重要。自同构 称为主对合(main involution)或次数对合(grade involution)。此
称为主对合(main involution)或次数对合(grade involution)。此 -分次中的纯元素,即偶部或奇部的元素,分别称为偶元和奇元。
-分次中的纯元素,即偶部或奇部的元素,分别称为偶元和奇元。
当特征非 时,由于
时,由于 与外代数
与外代数 有典范同构,
有典范同构, 作为向量空间,承继
作为向量空间,承继 的
的 -分次和
-分次和 -分次。[d]然而,该分次仅为向量空间分次,而非代数分次。换言之,克里福乘积并不遵守该
-分次。[d]然而,该分次仅为向量空间分次,而非代数分次。换言之,克里福乘积并不遵守该 -分次或
-分次或 -分次,仅遵守上段的
-分次,仅遵守上段的 -分次:例如,若
-分次:例如,若 ,则
,则 ,但
,但 ,而不在
,而不在 中。不过此等分次之间有自然的联系:
中。不过此等分次之间有自然的联系: 。更甚者,克里福代数有
。更甚者,克里福代数有 -滤过:
-滤过:

克里福数的次数通常指 -分次的次数。
-分次的次数。
克里福代数的偶子代数![{\displaystyle \mathrm {Cl} ^{[0]}(V,Q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b95e0638819f9c71415acd8045a5b8df5eda754) 本身亦同构于某个克里福代数。[e][f]若
本身亦同构于某个克里福代数。[e][f]若 为具有非零范数
为具有非零范数 的向量
的向量 与子空间
与子空间 的正交直和,则
的正交直和,则![{\displaystyle \mathrm {Cl} ^{[0]}(V,Q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b95e0638819f9c71415acd8045a5b8df5eda754) 同构于
同构于 ,其中
,其中 为二次型
为二次型 乘上
乘上 ,并限制到
,并限制到 。作为例子,以上结论在实域上推出:
。作为例子,以上结论在实域上推出:
![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}(\mathbb {R} )\cong {\begin{cases}\operatorname {Cl} _{p,q-1}(\mathbb {R} ),&q>0,\\\operatorname {Cl} _{q,p-1}(\mathbb {R} ),&p>0.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f26b903ab34e6843840ad77e22c9789d7e1cf97d)
在 负定的情况下,上式给出包含关系
负定的情况下,上式给出包含关系 ,延伸序列
,延伸序列

类似可证,在复域上,  的偶子代数同构于
的偶子代数同构于 。
。
除自同构 外,克里福代数的分析中,还有两个重要的反自同构。记得张量代数
外,克里福代数的分析中,还有两个重要的反自同构。记得张量代数 有将全部乘法次序反转的反自同构:
有将全部乘法次序反转的反自同构:

由于理想 在该反转下不变,该反转也定义
在该反转下不变,该反转也定义 上的反自同构,称为转置或反转,记为
上的反自同构,称为转置或反转,记为 。转置为反自同构,即有
。转置为反自同构,即有 。上述定义中,并未用到
。上述定义中,并未用到 -分次,故可复合自同构
-分次,故可复合自同构 与转置,而得另一个反自同构。新的反自同构称为克里福共轭,记为
与转置,而得另一个反自同构。新的反自同构称为克里福共轭,记为 。以符号表示:
。以符号表示:

两个反自同构中,转置更本质。[g]
此三种运算皆是对合。此外,其对 -分次纯元的作用皆是乘上
-分次纯元的作用皆是乘上 ,且符号仅取决于次数
,且符号仅取决于次数 。换言之,若
。换言之,若 是
是 次纯元,则
次纯元,则

其中符号载于下表:

|
 |
 |
 |
 |
…
|

|
 |
 |
 |
 |

|

|
 |
 |
 |
 |

|

|
 |
 |
 |
 |

|
当特徴非 时,
时, 上的二次型
上的二次型 可以延拓成
可以延拓成 上的二次型(同样记为
上的二次型(同样记为 )。该延拓可用以下不取决于基的方式定义:
)。该延拓可用以下不取决于基的方式定义:

其中 表示
表示 的纯量部分(
的纯量部分( -分次的零次项)。可以证明,对于
-分次的零次项)。可以证明,对于 的元素
的元素 ,有
,有

但上式对 的其他元素不一定成立。
的其他元素不一定成立。
在 上,与
上,与 相伴的对称双线性型由下式定义:
相伴的对称双线性型由下式定义:

可以验算,若限制在 上,则该双线性型化为
上,则该双线性型化为 上原有的双线性型。在
上原有的双线性型。在 上,该双线性型非退化当且仅当其限制在
上,该双线性型非退化当且仅当其限制在 上非退化。
上非退化。
关于此纯量积,左(右)乘 与右(左)乘
与右(左)乘 互为伴随。换言之,
互为伴随。换言之,

且

本节假设域的特征非 ,向量空间
,向量空间 为有限维,且二次型
为有限维,且二次型 非退化。若矩阵代数的系数取自某个中心为
非退化。若矩阵代数的系数取自某个中心为 的有限维除代数,则该矩阵代数称为
的有限维除代数,则该矩阵代数称为 上的中心单代数。例如,实域上的中心单代数可能是实域上的矩阵代数,也可能是四元数代数上的矩阵代数。有下列结论:
上的中心单代数。例如,实域上的中心单代数可能是实域上的矩阵代数,也可能是四元数代数上的矩阵代数。有下列结论:
- 若
 的维数为偶数,则
的维数为偶数,则 是
是 上的中心单代数。
上的中心单代数。
- 若
 的维数为偶数,则偶子代数
的维数为偶数,则偶子代数![{\displaystyle \mathrm {Cl} ^{[0]}(V,Q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b95e0638819f9c71415acd8045a5b8df5eda754) 或是
或是 的二次扩张上的中心单代数,或是
的二次扩张上的中心单代数,或是 上两个同构的中心单代数的直和。
上两个同构的中心单代数的直和。
- 若
 的维数为奇数,则
的维数为奇数,则 或是
或是 的二次扩张上的中心单代数,或是
的二次扩张上的中心单代数,或是 上两个同构的中心单代数的直和。
上两个同构的中心单代数的直和。
- 若
 的维数为奇数,则偶子代数
的维数为奇数,则偶子代数![{\displaystyle \mathrm {Cl} ^{[0]}(V,Q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b95e0638819f9c71415acd8045a5b8df5eda754) 是
是 上的中心单代数。
上的中心单代数。
克里福代数的结构可从以下结果推导出:假设 有偶数维,且有非退化的双线性型,其行列式为
有偶数维,且有非退化的双线性型,其行列式为 ,又设
,又设 为另一个向量空间,亦配备二次型,则
为另一个向量空间,亦配备二次型,则 的克里福代数同构于
的克里福代数同构于 的克里福代数与
的克里福代数与 的克里福代数的张量积。(后者仍是向量空间
的克里福代数的张量积。(后者仍是向量空间 ,但其上的二次型要乘上因子
,但其上的二次型要乘上因子 。)在实域上,上述结果推出:
。)在实域上,上述结果推出:



该些公式可用作找出所有实克里福代数和复克里福代数的结构,详见克里福代数的分类。
值得注意,克里福代数的森田等价类(即其整个表示论:该代数上的模范畴的加性等价类)只取决于其符号 。此为一种代数形式的博特周期性。
。此为一种代数形式的博特周期性。
利普希茨群(又称为[4]:126克里福群或克里福-利普希茨群)由鲁道夫·利普希茨发现。[6]:220
本节中,设 为有限维向量空间,而二次型
为有限维向量空间,而二次型 非退化。
非退化。
克里福代数的可逆元群以“扭转共轭”的方式作用在克里福代数上:所谓 扭转共轭作用在
扭转共轭作用在 上,结果便是
上,结果便是 ,其中
,其中 是上文定义的主对合。
是上文定义的主对合。
利普希茨群 定义为所有满足
定义为所有满足

的可逆元 的集合。换言之,要求
的集合。换言之,要求 的扭转共轭稳定化所有向量组成的集合。[9]
的扭转共轭稳定化所有向量组成的集合。[9]
上式说明,该群作用可以限制成向量空间 上的群作用,且其保持二次型
上的群作用,且其保持二次型 ,故给出利普希茨群到正交群的同态。利普希茨群包含所有令
,故给出利普希茨群到正交群的同态。利普希茨群包含所有令 在
在 中可逆的元素
中可逆的元素 ,而此等元素作用在
,而此等元素作用在 上的效果为反射
上的效果为反射

(特征为 时,此种映射称为错切而非反射。)
时,此种映射称为错切而非反射。)
若 为有限维实向量空间,并配备非退化二次型,则利普希茨群满射到
为有限维实向量空间,并配备非退化二次型,则利普希茨群满射到 关于该二次型的正交群(根据嘉当-迪厄多内定理),且核恰好包含
关于该二次型的正交群(根据嘉当-迪厄多内定理),且核恰好包含 的所有非零元,故有下列短正合列
的所有非零元,故有下列短正合列


其中 是
是 的偶子群。
的偶子群。
其他域上,或当二次型退化时,该映射未必满,而旋量范数描述其不满程度。
对任意特征,利普希茨群上的旋量范数 由下式定义:
由下式定义:

其为由利普希茨群射去非零元素的乘法群 的同态。当
的同态。当 视为克里福代数的子空间时,
视为克里福代数的子空间时, 在
在 上等于与
上等于与 原有的二次型。若干作者采用不同的定义,以致在
原有的二次型。若干作者采用不同的定义,以致在 上,其定义与上述定义相差
上,其定义与上述定义相差 、
、 、
、 倍。只要特征不为
倍。只要特征不为 ,此差异并不重要。
,此差异并不重要。
 中的非零元素的旋量范数是在非零平方子群
中的非零元素的旋量范数是在非零平方子群 中,所以,若
中,所以,若 有限维且其上的二次型非退化,则有同态从
有限维且其上的二次型非退化,则有同态从 的正交群映去
的正交群映去 ,亦称为旋量范数。对任意向量
,亦称为旋量范数。对任意向量 ,关于
,关于 (
( 是关于二次型而言)反射的旋量范数在
是关于二次型而言)反射的旋量范数在 中的像为
中的像为 。此性质唯一确定正交群上的旋量范数。故有正合列:
。此性质唯一确定正交群上的旋量范数。故有正合列:

注意在特征为 时,群
时,群 只有一个元素。
只有一个元素。
若从代数群的伽罗瓦上同调考虑,旋量范数是上同调的连接同态。其含义是,以 表示1的平方根组成的代数群(若域的特征不为
表示1的平方根组成的代数群(若域的特征不为 ,则该群大致就是二元群,且其伽罗瓦作用平凡),则短正合列
,则该群大致就是二元群,且其伽罗瓦作用平凡),则短正合列

给出上同调层面的长正合列,其起始一段为

代数群的 系数零阶伽罗瓦上同调即其
系数零阶伽罗瓦上同调即其 值点旳群:
值点旳群: ,而
,而  ,故也能从长正合列推导出上段的正合列
,故也能从长正合列推导出上段的正合列

其中旋量范数为连接同态 。
。
本节假设 有限维,且其双线性型非退化。
有限维,且其双线性型非退化。
Pin群 为利普希茨群
为利普希茨群 中,旋量范数为
中,旋量范数为 的元素组成的子群。类似地,旋量群
的元素组成的子群。类似地,旋量群 为
为 中,迪克森不变量为
中,迪克森不变量为 的元素组成的子群。当特征非
的元素组成的子群。当特征非 时,该些元素即行列式为
时,该些元素即行列式为 的元素。旋量群在Pin群的指数通常为
的元素。旋量群在Pin群的指数通常为 。
。
前一节说明,利普希茨群有到正交群的满同态。定义特殊正交群为 的像。若
的像。若 的特征非
的特征非 ,则特殊正交群就是正交群中,行列式为
,则特殊正交群就是正交群中,行列式为 的元素的子群。若
的元素的子群。若 的特征为
的特征为 ,则正交群所有元素的行列式皆为
,则正交群所有元素的行列式皆为 ,而特殊正交群为迪克森不变量为
,而特殊正交群为迪克森不变量为 的元素的子群。
的元素的子群。
也有从Pin群到正交群的同态。其像由旋量范数为 的元素组成,而核则由
的元素组成,而核则由 和
和 组成(故其阶为
组成(故其阶为 ,除非特征为
,除非特征为 )。类似有由
)。类似有由 的旋量群到其特殊正交群的同态。
的旋量群到其特殊正交群的同态。
当 为实正定或负定空间时,旋量群有满同态射到特殊正交群上,且在
为实正定或负定空间时,旋量群有满同态射到特殊正交群上,且在 至少
至少 维时,旋量群单连通。更甚者,此满同态的核为
维时,旋量群单连通。更甚者,此满同态的核为 。故此时,旋量群
。故此时,旋量群 为
为 的二重复叠。然而,旋量群在一般情况下未必单连通:若
的二重复叠。然而,旋量群在一般情况下未必单连通:若 为
为 ,其中
,其中 皆至少为
皆至少为 ,则旋量群并不单连通。此情况下,代数群
,则旋量群并不单连通。此情况下,代数群 作为代数群仍然单连通,但其实值点群
作为代数群仍然单连通,但其实值点群 则不再单连通。
则不再单连通。
在 为偶时,克里福代数
为偶时,克里福代数 可表示成
可表示成 维的(复)矩阵代数。限制到群
维的(复)矩阵代数。限制到群 ,则得到同一维数的Pin群的复表示,称为旋量表示。若再限制到旋量群
,则得到同一维数的Pin群的复表示,称为旋量表示。若再限制到旋量群 上,则该表示分解成两个半旋量表示(half spin representations,又称外尔表示,Weyl representations)的直和,每个半旋量表示有
上,则该表示分解成两个半旋量表示(half spin representations,又称外尔表示,Weyl representations)的直和,每个半旋量表示有 维。
维。
若 为奇,则克里数代数
为奇,则克里数代数 为两个矩阵代数的直和,每个有
为两个矩阵代数的直和,每个有 维,且皆为Pin群
维,且皆为Pin群 的表示。限制到旋量群
的表示。限制到旋量群 时,两个矩阵代数变得同构,故旋量群有
时,两个矩阵代数变得同构,故旋量群有 维的复旋量表示。
维的复旋量表示。
更一般而言,任何域上的旋量群和Pin群都有相似的表示,其结构取决于对应的克里福代数的结构:每当克里福代数有因子为某个除代数上的矩阵代数,其Pin群和旋量群就有该除代数上的对应表示。在实域的例子,参见旋量条目。
为描述实旋量表示,需先明白旋量群如何位处克里福代数中。Pin群 为
为 中,可写成单位向量之积的可逆元素的集合:
中,可写成单位向量之积的可逆元素的集合:

若考虑克里福代数的矩阵表示,则pin群的元素为任意多个反射(见上文)之积,是整个正交群 的覆叠。而旋量群的元素则是
的覆叠。而旋量群的元素则是 中,偶数支单位向量之积。所以,根据嘉当-迪厄多内定理,旋量群是旋转群
中,偶数支单位向量之积。所以,根据嘉当-迪厄多内定理,旋量群是旋转群 的覆叠。
的覆叠。
设 为自同构,其将纯向量
为自同构,其将纯向量 映至
映至 ,则
,则 为
为 中,
中, 的不动点组成的子群。又设
的不动点组成的子群。又设
![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}=\{x\in \operatorname {Cl} _{p,q}\mid \alpha (x)=x\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e214b8b455c0610747a107adad00e2c3573ca61)
(其元素正是 的偶次元素。)则旋量群包含于
的偶次元素。)则旋量群包含于![{\displaystyle \mathrm {Cl} _{p,q}^{[0]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50aac8d6b975f2c3da4d598216e6b5082f83ed08) 。
。
 的不可约表示可以限制成pin群的表示。反之,由于pin群由单位向量生成,其所有不可约表示皆可如此导出,故两者有一样的不可约表示。同理,旋量群与
的不可约表示可以限制成pin群的表示。反之,由于pin群由单位向量生成,其所有不可约表示皆可如此导出,故两者有一样的不可约表示。同理,旋量群与![{\displaystyle \mathrm {Cl} _{p,q}^{[0]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50aac8d6b975f2c3da4d598216e6b5082f83ed08) 有同样的不可约表示。
有同样的不可约表示。
要将pin群的表示分类,需要用到克里福代数的分类。至于旋量群的表示(与偶子代数的表示一样),可以使用下列同构(见上文):
![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}\cong \operatorname {Cl} _{p,q-1},\quad q>0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f577d7e3b1ee705c0a49d4cc02bc3c4a500cd83f)
![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}\cong \operatorname {Cl} _{q,p-1},\quad p>0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3f54de96cfa5fa50cc445b55dfeba1ebca01991)
从而得知,符号 的旋量群表示就是符号
的旋量群表示就是符号 或
或 的pin群表示。
的pin群表示。
外代数在微分几何可用作定义光滑流形上的微分形式丛。在(伪)黎曼流形的情况,每个切空间上配备自然的二次型(由度规张量导出)。所以,如同外丛,可以定义克里福丛。在黎曼几何,克里福丛有若干重要应用,例如其与旋量流形、相伴的旋量丛、 流形的关联。
流形的关联。
克里福代数在物理有若干重要应用。物理学家通常认定克里福代数具有一组基,其由狄拉克矩阵 生成。此种矩阵满足关系式
生成。此种矩阵满足关系式

其中 为记号
为记号 (或
(或 ,度量记号的两种等价选取)的二次型的矩阵。上列关系式恰好是定义实克里福代数
,度量记号的两种等价选取)的二次型的矩阵。上列关系式恰好是定义实克里福代数 的关系式,而该代数的复化
的关系式,而该代数的复化 根据克里福代数的分类,同构于
根据克里福代数的分类,同构于 复矩阵的代数
复矩阵的代数 。然而,在此用法下,仍需保留
。然而,在此用法下,仍需保留 的写法,因为将双线性型变成标准型的变换不属时空的洛伦兹变换。
的写法,因为将双线性型变成标准型的变换不属时空的洛伦兹变换。
所以,物理使用的时空克里福代数比 有更多结构。例如,有额外指明一族允许的变换,即洛伦兹变换。视乎用途,例如希望框架能容纳多少理论,不一定一开始便要复化,但在量子力学,为使李代数
有更多结构。例如,有额外指明一族允许的变换,即洛伦兹变换。视乎用途,例如希望框架能容纳多少理论,不一定一开始便要复化,但在量子力学,为使李代数 的旋量表示能包含于克里福代数中,通常都须考虑复克里福代数。以下列出定义该旋量李代数的关系式以供参考:
的旋量表示能包含于克里福代数中,通常都须考虑复克里福代数。以下列出定义该旋量李代数的关系式以供参考:
![{\displaystyle {\begin{aligned}\sigma ^{\mu \nu }&=-{\frac {i}{4}}\left[\gamma ^{\mu },\,\gamma ^{\nu }\right],\\\left[\sigma ^{\mu \nu },\,\sigma ^{\rho \tau }\right]&=i\left(\eta ^{\tau \mu }\sigma ^{\rho \nu }+\eta ^{\nu \tau }\sigma ^{\mu \rho }-\eta ^{\rho \mu }\sigma ^{\tau \nu }-\eta ^{\nu \rho }\sigma ^{\mu \tau }\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b5881264248f2f1787c4d1d2c4de84dd1678754)
上式按照 记号的约定,因此能放入
记号的约定,因此能放入 。[10]
。[10]
狄拉克矩阵最早由保罗·狄拉克写出,其时他正尝试写出电子的相对论性一阶波动方程,并试图给出由克里福代数到复矩阵代数的明确同构。该些矩阵后来用作定义狄拉克方程式和引入狄拉克算子。在量子场论中,整个克里福代数以Dirac field bilinear的形式出现。
使用克里福代数来描述量子理论,推动者有Mario Schönberg[h]、David Hestenes(几何微积分方面)、戴维·玻姆和Basil Hiley及同事(克里福代数的分层)、Elio Conte等。[11][12]
电脑视觉方面,克里福代数适用于辨认和分类动作。米基·洛迪古斯(Mikel Rodriguez)及合作者[13]提出用克里福嵌入,将传统的最大平均关联高度滤子(Maximum Average Correlation Height filter, MACH filter)推广,套用于影片(3D时空体积)以及向量值数据,例如光流。向量值数据需以克里福傅立叶变换分析。基于该些向量,能在克里福傅立叶域中,合成出动作滤子,然后用克里福关联来辨认动作。论文作者用克里福嵌入,分辨出传统剧情长片和体育广播的常见动作,以论证其方法有效。
- 本条目只考虑域上的向量空间的克里福代数,但同样可定义任何单位结合交换环上的模的克里福代数。[3]
- 亦在克里福代数的定义中,将二次型推广成更高次的映射。[14]
克里福代数和几何代数,以及相关的跨学科研究,是活跃的研究主题,且有广泛的应用。此学科的学术会议包括克里福代数及其在数学物理的应用国际会议(ICCA) (页面存档备份,存于互联网档案馆)及几何代数在电脑科学及工程学的应用(AGACSE) (页面存档备份,存于互联网档案馆)两个系列。期刊包括斯普林格出版的《应用克里福代数进展》。
- ^ 研究实克里福代数且偏好正定二次型者(尤其研究指标理论者),有时在基本克里福恒等式中使用不同的符号。换言之,其取
 。代
。代 为
为 ,便可切换两种约定。
,便可切换两种约定。
- ^ [4]明确指出映射
 (引文作
(引文作 )是克里福代数结构的一部分,其定义写作:“有序对
)是克里福代数结构的一部分,其定义写作:“有序对 为二次空间
为二次空间 的克里福代数,若
的克里福代数,若 作为代数是由
作为代数是由 和
和 生成,且
生成,且 满足:对所有
满足:对所有 ,有
,有 。”
。”
- ^ 故群代数
![{\displaystyle K[\mathbb {Z} /2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5a75e48de8b88ea9f7f75bc179a736ff80e9fde) 为半单,且克里福代数可分解成主对合的特征空间。
为半单,且克里福代数可分解成主对合的特征空间。
- ^ 此处的
 -分次,仅是将
-分次,仅是将 的
的 -分次添加负指标处的零子空间。
-分次添加负指标处的零子空间。
- ^ 严格而言,因为未指明克里福代数定义中的向量空间,所以该同构仅是代数同构,而非克里福代数同构。
- ^ 仍假设特征非
 。
。
- ^ 若在克里福代数的定义中,约定的符号不同(多一个负号),则反之,即共轭更本质。一般而言,共轭与转置的含义会因约定的符号不同而互换。例如,本条目采用的定义中,向量的逆元为
 ,但约定相反的符号时,则有
,但约定相反的符号时,则有 。
。
- ^ 见A. O. Bolivar,
Classical limit of fermions in phase space, J. Math. Phys. 42, 4020 (2001) doi:10.1063/1.1386411在"The Grassmann–Schönberg algebra
 "一节描述,Schönberg在1956年和1957年出版的论文。
"一节描述,Schönberg在1956年和1957年出版的论文。
- ^ Clifford, W.K. Preliminary sketch of bi-quaternions. Proc. London Math. Soc. 1873, 4: 381–395 (英语).
- ^ Clifford, W.K. Tucker, R. , 编. Mathematical Papers. London: Macmillan. 1882 (英语).
- ^ 3.0 3.1 Oziewicz, Z.; Sitarczyk, Sz. Parallel treatment of Riemannian and symplectic Clifford algebras. Micali, A.; Boudet, R.; Helmstetter, J. (编). Clifford Algebras and their Applications in Mathematical Physics. Kluwer. 1992: 83 [2021-08-05]. ISBN 0-7923-1623-1. (原始内容存档于2021-08-05) (英语).
- ^ 4.0 4.1 Vaz, J.; da Rocha, R., An Introduction to Clifford Algebras and Spinors, Oxford University Press, 2016, ISBN 978-0-19-878292-6 (英语)
- ^ P. Lounesto, Counterexamples in Clifford algebras with CLICAL, Clifford Algebras with Numeric and Symbolic Computations, 1996: 3–30, ISBN 978-1-4615-8159-8, doi:10.1007/978-1-4615-8157-4_1 (英语) ,或删节版 (页面存档备份,存于互联网档案馆)
- ^ 6.0 6.1 Lounesto, Pertti, Clifford algebras and spinors, Cambridge University Press, 2001, ISBN 978-0-521-00551-7, doi:10.1017/CBO9780511526022 (英语)
- ^ McCarthy, J.M. An Introduction to Theoretical Kinematics. MIT Press. 1990: 62–65 [2021-08-06]. ISBN 978-0-262-13252-7. (原始内容存档于2021-08-06) (英语).
- ^ Bottema, O.; Roth, B. Theoretical Kinematics. Dover. 2012 [1979] [2021-08-06]. ISBN 978-0-486-66346-3. (原始内容存档于2021-08-06) (英语).
- ^ Perwass, Christian, Geometric Algebra with Applications in Engineering, Springer Science & Business Media, 2009, Bibcode:2009gaae.book.....P, ISBN 978-3-540-89068-3 (英语) , §3.3.1
- ^ Weinberg, S., The Quantum Theory of Fields 1, Cambridge University Press, 2002, ISBN 0-521-55001-7 (英语)
- ^ Conte, Elio. A Quantum-Like Interpretation and Solution of Einstein, Podolsky, and Rosen Paradox in Quantum Mechanics. 14 Nov 2007. arXiv:0711.2260
 [quant-ph] (英语).
[quant-ph] (英语).
- ^ Conte, Elio. On some considerations of mathematical physics: May we identify Clifford algebra as a common algebraic structure for classical diffusion and Schrödinger equations?. Adv. Studies Theor. Phys. 2012, 6 (26): 1289–1307 (英语).
- ^ Rodriguez, Mikel; Shah, M. Action MACH: A Spatio-Temporal Maximum Average Correlation Height Filter for Action Classification. Computer Vision and Pattern Recognition (CVPR). 2008 (英语).
- ^
Darrell E. Haile. On the Clifford Algebra of a Binary Cubic Form. American Journal of Mathematics (The Johns Hopkins University Press). Dec 1984, 106 (6): 1269–1280. JSTOR 2374394. doi:10.2307/2374394 (英语).

 [quant-ph] (英语).
[quant-ph] (英语).










































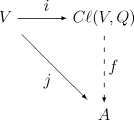
























































![{\displaystyle \mathrm {Cl} _{0,3}^{[0]}(\mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6541725197b4f192001bd32ca1cf8b678d576da5)

















![{\displaystyle \mathrm {Cl} ^{[0]}(\mathbb {R} ^{4},d)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99eff326ee15b18fc9a58606715d26fb85642933)









![{\displaystyle K[x]/(x^{2}-a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c62c3e9a4da297f0a0758ff5849fbfe553242cc)





































![{\displaystyle \operatorname {Cl} (V,Q)=\operatorname {Cl} ^{[0]}(V,Q)\oplus \operatorname {Cl} ^{[1]}(V,Q),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f839fb22e8ff47a3cd64ae06d9a6338584ff0a5)
![{\displaystyle \operatorname {Cl} ^{[i]}(V,Q)=\left\{x\in \operatorname {Cl} (V,Q)\mid \alpha (x)=(-1)^{i}x\right\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6902ed1e7c0361df4271000a56e7b76c029990e)
![{\displaystyle \operatorname {Cl} ^{[i]}(V,Q)\operatorname {Cl} ^{[j]}(V,Q)=\operatorname {Cl} ^{[i+j]}(V,Q),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25f34257a1d5cb5d629f65bf4806f4644ce0fb33)
![{\displaystyle \mathrm {Cl} ^{[0]}(V,Q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b95e0638819f9c71415acd8045a5b8df5eda754)
![{\displaystyle \mathrm {Cl} ^{[1]}(V,Q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f04cddd1b4026240bc7face04ef5d2c4f25639a)













![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}(\mathbb {R} )\cong {\begin{cases}\operatorname {Cl} _{p,q-1}(\mathbb {R} ),&q>0,\\\operatorname {Cl} _{q,p-1}(\mathbb {R} ),&p>0.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f26b903ab34e6843840ad77e22c9789d7e1cf97d)























































































![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}=\{x\in \operatorname {Cl} _{p,q}\mid \alpha (x)=x\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e214b8b455c0610747a107adad00e2c3573ca61)
![{\displaystyle \mathrm {Cl} _{p,q}^{[0]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50aac8d6b975f2c3da4d598216e6b5082f83ed08)
![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}\cong \operatorname {Cl} _{p,q-1},\quad q>0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f577d7e3b1ee705c0a49d4cc02bc3c4a500cd83f)
![{\displaystyle \operatorname {Cl} _{p,q}^{[0]}\cong \operatorname {Cl} _{q,p-1},\quad p>0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3f54de96cfa5fa50cc445b55dfeba1ebca01991)














![{\displaystyle {\begin{aligned}\sigma ^{\mu \nu }&=-{\frac {i}{4}}\left[\gamma ^{\mu },\,\gamma ^{\nu }\right],\\\left[\sigma ^{\mu \nu },\,\sigma ^{\rho \tau }\right]&=i\left(\eta ^{\tau \mu }\sigma ^{\rho \nu }+\eta ^{\nu \tau }\sigma ^{\mu \rho }-\eta ^{\rho \mu }\sigma ^{\tau \nu }-\eta ^{\nu \rho }\sigma ^{\mu \tau }\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b5881264248f2f1787c4d1d2c4de84dd1678754)










![{\displaystyle K[\mathbb {Z} /2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5a75e48de8b88ea9f7f75bc179a736ff80e9fde)


