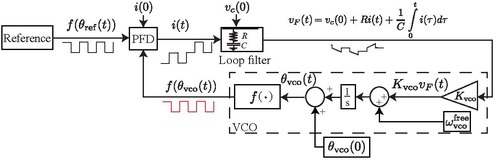
电荷泵锁相回路

电荷泵锁相回路

电荷泵锁相回路（Charge-pump phase-locked loop）简称CP-PLL，是一种鉴相器适用于方波输入信号的锁相回路。CP-PLL可以快速的锁定到输入信号的相位，可以达到很低的稳态相位误差。

鉴相器（PFD）

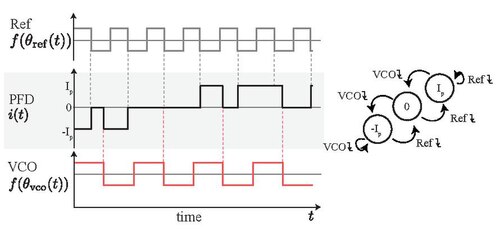
鉴相器动态

鉴相器（PFD）是由参考信号（Ref）以及受控输出（VCO）信号的下缘所触发。PFD $i(t)$的输出信号只有三个状态：0, $+I_{p}$,和$-I_{p}$。 参考信号的下缘会使PFD切换到较高的状态，若PFD已经在$+I_{p}$就不会变动。 VCO信号的下缘会使PFD切换到较低的状态，若PFD已经在$-I_{p}$就不会变动。 若二个信号的下缘同时出现，PFD会切换到0。

CP-PLL的数学模型

第一个二阶CP-PLL的数学模型是由佛洛依德·加德纳在1980年提出的。M. van Paemel在1994年提出了不考虑VCO过载（overload）的非线性模型，N. Kuznetsov等人在2019年优化该模型。也有学者在推导考虑VCO过载的CP-PLL解析解数学模型。

CP-PLL的数学模型可以针对一些参数进行解析的预估，例如hold-in范围（在VCO没有过载的情形下，可能进行锁相的输入信号频率范围），及捕获范围（pull-in range，在CP-PLL任意初始状态下，CP-PLL最终可以锁相的输入信号频率范围）。

二阶CP-PLL的连续时间线性模型以及加德纳的猜想

加德纳的分析是以以下的近似为基础：每个参考信号的周期内，PFD非零的时间区间为

$t_{p}=|\theta _{e}|/\omega _{\rm {ref}},\ \theta _{e}=\theta _{\rm {ref}}-\theta _{\rm {vco}}.$

CP-PLL的PDF平均输出为

$i_{d}=I_{p}\theta _{e}/2\pi$

对应的传递函数为

$I_{d}(s)=I_{p}\theta _{e}(s)/2\pi$

若用滤波器传递函数$F(s)=R+{\frac {1}{Cs}}$以及VCO传递函数$\theta _{\rm {vco}}(s)=K_{\rm {vco}}I_{d}(s)F(s)/s$，可以得到加德纳的二阶CP-PLL线性近似平均模型:

${\frac {\theta _{e}(s)}{\theta _{\rm {ref}}(s)}}={\frac {2\pi s}{2\pi s+K_{\rm {vco}}I_{p}\left(R+{\frac {1}{Cs}}\right)}}.$

佛洛依德·加德纳在1980年以上述的理解，提出了猜想：“实际电荷泵锁相回路的暂态响应，预期会和等效传统PLL的暂态响应几乎相同。”（加德纳对CP-PLL的猜想）。 依照加德纳的结果，也类似Egan在type 2 APLL捕获范围的猜想，Amr M. Fahim在其书中猜想：为了要达到无限大的捕获范围，CP-PLL的回路滤波器需要使用主动滤波器（Fahim-Egan在type II CP-PLL捕获范围的猜想）。

二阶CP-PLL的连续时间非线性模型

为了简化推导，但不失去通用性，假设VCO和参考信号在其相位为整数时为其下降缘。 令参考信号第一个下降缘的时间为$t=0$。 PFD状态$i(0)$会依PFD的初始状态$i(0-)$，VCO的初始相位移$\theta _{vco}(0)$，以及参考信号$\theta _{ref}(0)$的值而不同。

若利用电阻和电容制作纯PI（比例积分）的滤波器，其输入电流$i(t)$和输出电压$v_{F}(t)$的关系为

${\begin{aligned}v_{F}(t)=v_{c}(0)+Ri(t)+{\frac {1}{C}}\int \limits _{0}^{t}i(\tau )d\tau \end{aligned}}$

其中$R>0$是电阻，$C>0$是电感。 $v_{c}(t)$是电容器的电压。 控制信号$v_{F}(t)$会调整VCO频率：

${\begin{aligned}{\dot {\theta }}_{vco}(t)=\omega _{vco}(t)=\omega _{vco}^{\text{free}}+K_{vco}v_{F}(t),\end{aligned}}$

其中$\omega _{vco}^{\text{free}}$是VCO的自由运行频率 （也就是$v_{F}(t)\equiv 0$)，$K_{vco}$是VCO增益（灵敏度）、$\theta _{vco}(t)$是VCO相位。 最后，CP-PLL连续时间非线性数学模型如下

${\begin{aligned}{\dot {v}}_{c}(t)={\tfrac {1}{C}}i(t),\quad {\dot {\theta }}_{vco}(t)=\omega _{vco}^{\text{free}}+K_{vco}(Ri(t)+v_{c}(t))\end{aligned}}$

其中有以下的不连续分段常数非线性

$i(t)=i{\big (}i(t-),\theta _{ref}(t),\theta _{vco}(t){\big )}$

初始条件为${\big (}v_{c}(0),\theta _{vco}(0){\big )}$. 此模型是非线性、非自主式、不连续的开关系统。

二阶CP-PLL的离散时间非线性模型

在时间区间内的PFD动态

假设参考信号频率为常数: $\theta _{ref}(t)=\omega _{ref}t={\frac {t}{T_{ref}}},$ 其中$T_{ref}$、$\omega _{ref}$和$\theta _{ref}(t)$是参考资料的周期、频率和相位。

令$t_{0}=0$， 这表示$t_{0}^{\rm {middle}}$是第一个PFD输出为0的时间 （若$i(0)=0$，则$t_{0}^{\rm {middle}}=0$） 且$t_{1}$是VCO或参考信号的第一个下降缘。 其且，可以定义对应的递减数列$\{t_{k}\}$、$\{t_{k}^{\rm {middle}}\}$，其中$k=0,1,2...$。

令$t_{k}<t_{k}^{\rm {middle}}$. 则在$t\in [t_{k},t_{k}^{\rm {middle}})$时，${\text{sign}}(i(t))$是非零的常数（$\pm 1$）。 令$\tau _{k}$为PFD脉波宽度（PFD输出为非零长度的时间区间）乘以PFD输出的正负号：

$\tau _{k}=(t_{k}^{\rm {middle}}-t_{k}){\text{sign}}(i(t))$ for $t\in [t_{k},t_{k}^{\rm {middle}})$

$\tau _{k}=0$ for $t_{k}=t_{k}^{\rm {middle}}$

若VCO的下降缘在参考信号的下降缘之前，则$\tau _{k}<0$，反之，可得$\tau _{k}>0$。$\tau _{k}$可以看出二个信号下降缘的先后顺序。在$(t_{k}^{\rm {middle}},t_{k+1})$区间内，PFD输出为零，PFD $i(t)\equiv 0$：

$v_{F}(t)\equiv v_{k}$ for $t\in [t_{k}^{\rm {middle}},t_{k+1})$.

将$(\tau _{k},v_{k})$变成下式的变数变换 $p_{k}={\frac {\tau _{k}}{T_{\rm {ref}}}},u_{k}=T_{\rm {ref}}(\omega _{\rm {vco}}^{\text{free}}+K_{\rm {vco}}v_{k})-1,$ 可以让参数减至二个： $\alpha =K_{\rm {vco}}I_{p}T_{\rm {ref}}R,\beta ={\frac {K_{\rm {vco}}I_{p}T_{\rm {ref}}^{2}}{2C}}.$

此处$p_{k}$是正规化的相位偏移，$u_{k}+1$是VCO频率 $\omega _{\rm {vco}}^{\text{free}}+K_{\rm {vco}}v_{k}$相对于参考频率${\frac {1}{T_{\rm {ref}}}}$的比例。

最后，不考虑VCO过载的二阶CP-PLL离散时间模型如下

${\begin{aligned}&u_{k+1}=u_{k}+2\beta p_{k+1},\\&p_{k+1}={\begin{cases}{\frac {-(u_{k}+\alpha +1)+{\sqrt {(u_{k}+\alpha +1)^{2}-4\beta c_{k}}}}{2\beta }},\quad {\text{ for }}p_{k}\geq 0,\quad c_{k}\leq 0,\\{\frac {1}{u_{k}+1}}-1+(p_{k}{\text{ mod }}1),\quad {\text{ for }}p_{k}\geq 0,\quad c_{k}>0,\\l_{k}-1,\quad {\text{ for }}p_{k}<0,\quad l_{k}\leq 1,\\{\frac {-(u_{k}+\alpha +1)+{\sqrt {(u_{k}+\alpha +1)^{2}-4\beta d_{k}}}}{2\beta }},\quad {\text{ for }}p_{k}<0,\quad l_{k}>1,\end{cases}}\end{aligned}}$

其中

${\begin{aligned}c_{k}=(1-(p_{k}{\text{ mod }}1))(u_{k}+1)-1,S_{l_{k}}=-(u_{k}-\alpha +1)p_{k}+\beta p_{k}^{2},l_{k}={\frac {1-(S_{l_{k}}{\text{ mod }}1)}{u_{k}+1}},d_{k}=(S_{l_{k}}{\text{ mod }}1)+u_{k}.\end{aligned}}$

此离散时间模型只在$(u_{k}=0,p_{k}=0)$有一个稳态，可以估计hold-in范围和捕获范围。

若VCO过载，也就是${\dot {\theta }}_{\rm {vco}}(t)$为零， 或者是以下的式子 $(p_{k}>0,u_{k}<2\beta p_{k}-1)$或 $(p_{k}<0,u_{k}<\alpha -1)$, 则需要考虑额外的CP-PLL动态特性。 针对任何参数，只要VCO和参考信号的频率差够大，就会使VCO过载。 在实务上，需避免VCO的过载。

高阶CP-PLL的非线性模型

高阶CP-PLL非线性模型推导和超越方程有关，无法求得解析解，需要用近似的方式计算