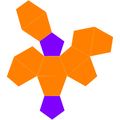
双五角锥台
 | |||
| 类别 | 双锥台 对偶詹森多面体 | ||
|---|---|---|---|
| 对偶多面体 | 双五角锥柱 | ||
| 性质 | |||
| 面 | 12 | ||
| 边 | 25 | ||
| 顶点 | 15 | ||
| 欧拉特征数 | F=12, E=25, V=15 (χ=2) | ||
| 组成与布局 | |||
| 面的种类 | 10个梯形、2个五边形 | ||
| 对称性 | |||
| 对称群 | D5h, [5,2], (*n55) | ||
| 特性 | |||
| 凸多面体 | |||
| 图像 | |||
| |||
在几何学中,双五角锥台是双锥台的一种,指二个五角锥台底面和底面相接所组成的立体,或是双五角锥被二个平行平面所截位于二个平面中间的立体图形。每个双五角锥台皆有10个梯形和2个五边形。
结构
[编辑]这个多面体可以借由将双五角锥的上下两个顶点切去构造。在康威多面体表示法中可以使用“切去五阶顶点”或“切去顶点图为五边形的顶点”的截角变换构造,即切去该立体所有顶点为五个多边形的公共顶点之顶点,在康威多面体表示法中以 t5 表示,又因原像是双五角锥,而双五角锥是五角柱的对偶,因此在康威多面体表示法中计为 dP5,其中d表示对偶多面体、P5表示五角柱。因此整个双五角锥台在康威多面体表示法中计为t5dP5[1][2]。
其他双五角锥台
[编辑]双五角锥台也可以借由将两个五角锥台底面对底面的组合来构造。对于这类构造方式,双五角锥台一般都是较大的底面互相接合所形成的凸多面体,若是由较小的底面接合的话,则会变成凹多面体,然而这种多面体也是双五角锥台,但是其与一般的双五角锥台不同,不能借由双五角锥切去上下的顶点构造。
对偶多面体
[编辑]双五角锥台的对偶多面体是双五角锥柱,是92种詹森多面体中的其中一个,其编号为J16,它可由一个正五角柱在两端各连接一个正多面体大小相同的五角锥面接合而成,与双五角锥(J12)有一定的相似程度。这92种詹森多面体最早在1996年由诺曼詹森命名并给予描述[3]。
双五角锥台的对偶为十五面体,具有15个面:10个三角形和5个正方形,20个边和10个顶点。
| 双五角锥台 的对偶多面体 |
对偶的展开图 |
|---|---|

|

|
应用
[编辑]在准晶的形成中,15个顶点的双五角锥台结构可以从大的五次对称或二十面体对称成核而得[4]。
相关多面体
[编辑]双五角锥台是由双五角锥被二个平面所截所形成的立体,与其相关的平截头体包括双五角锥只被一个平面所截形成的五角锥台锥,与五角锥柱或五角锥以不同方式截出的平截头体。
五角锥台锥
[编辑]在几何学中,五角锥台锥是一种将五角锥台与五角锥底面对底面相接的立体,或是与用一个平面截双五角锥后得到二个立体,一个是五角锥,另一个就是五角锥台锥。 五角锥台锥为自身对偶,具有11个面、20个边和11个顶点,其可以为詹森多面体正五角锥柱的对偶,由于大部分的五角锥台锥为自身对偶,而正五角锥柱这种詹森多面体属于五角锥台锥中的特例,但他们都具有相同的拓朴结构。拓朴结构有明显差异意味着两种多面体无法透过移动顶点位置、扭曲或伸缩来相互变换的多面体,例如五角锥台锥和双五角锥台,无论如何变形都无法互相变换,因此拓朴结构不同,但五角锥台锥和五角锥柱可以透过伸缩其中一个五角形面来彼此互换,因此五角锥台锥和五角锥柱在拓朴上并无明显差异。
五角锥台锥也是正五角锥柱的对偶,是一种十一面体,具有11个面:5个等腰三角形、5个等腰梯形和一个正三角形。
五角锥台
[编辑] | ||||
| 类别 | 锥台 | |||
|---|---|---|---|---|
| 对偶多面体 | 上下不对称的双五角锥 | |||
| 性质 | ||||
| 面 | 7 | |||
| 边 | 15 | |||
| 顶点 | 10 | |||
| 欧拉特征数 | F=7, E=15, V=10 (χ=2) | |||
| 组成与布局 | ||||
| 面的种类 | 5个梯形,2个五边形 | |||
| 对称性 | ||||
| 对称群 | C5v, [1,5], (*55) | |||
| 特性 | ||||
| 凸多面体 | ||||
| 图像 | ||||
| ||||
在几何学中,五角锥台是一种锥台或平截头体,五角锥台可以视作双五角锥台的一半,但更精确的定义为一个五角锥被两个平行平面所截后,位于两个平行平面之间的立体。五角锥台虽与双五角锥台相似,但拥有不同的对称性,且其对称性较双五角锥台低,也不属于任何一个詹森多面体的对偶多面体。
其他多面体
[编辑]双五角锥台是由五角柱先后经过对偶和截角变换而得,五角锥台亦是五角柱变形而来,而五角柱可以视为截角的五面形,五面形又是五边形二面体的对偶。其他与五边形二面体相关的多面体除了五角锥台之外,还有:
| 对称群:[5,2], (*522) | [5,2]+, (622) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|

|

|

| ||||||
| {5,2} | t{5,2} | r{5,2} | 2t{5,2}=t{2,5} | 2r{5,2}={2,5} | rr{5,2} | tr{5,2} | sr{5,2} | ||
| 半正对偶 | |||||||||

|

|

|

|

|

|

| |||
| V52 | V102 | V52 | V4.4.5 | V25 | V4.4.5 | V4.4.10 | V3.3.3.5 | ||
参见
[编辑]| 3 | 4 | 5 |
|---|---|---|
 双三角锥台 |
 双四角锥台 |
 双五角锥台 |
参考文献
[编辑]- ^ 乔治·威廉·哈特. Conway Notation for Polyhedra. [2014-12-20]. (原始内容存档于2014-11-29).
- ^ t5dP5, PolyHédronisme. [2022-08-09]. (原始内容存档于2023-11-08).
- ^ Norman W. Johnson, Convex polyhedra with regular faces, 加拿大数学学报, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8
- ^ Hofmeister, Herbert, Fivefold twinning in nanosized particles and nanocrystalline thin films – ubiquitous metastable structures (PDF), Materials Science Forum: 325–332, [2016-08-30], doi:10.4028/www.scientific.net/MSF.312-314.325, (原始内容存档 (PDF)于2011-05-15).