print "import modules...",
import sys
sys.stdout.flush()
import pickle
from mpl_toolkits.basemap import Basemap, shiftgrid, cm
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from netCDF4 import Dataset
print "ok"
# Lovecraft: 47:9'S 126:43'W
lovecraft_lat = -47.9
lovecraft_lon = -126.43
# August Derleth: 49:51'S 128:34'W
derleth_lat = -49.51
derleth_lon = -128.34
# Nemo point: 48:52.6'S 123:23.6'W
nemo_lat = -48.526
nemo_lon = -123.236
# The Bloop:
# Appears to be way too far from the Nemo point to be interesting in a R'lyeh context
# bransfield_strait_lat=-63
# bransfield_strait_lon=-59
# ross_sea_lat = -75
# ross_sea_lon = -175
# cape_adare_lat = -71.17
# cape_adare_lon = -170.14
# Not necessary, because the default projection is ortho,
# but can be useful if you want another one.
def equi(m, centerlon, centerlat, radius, *args, **kwargs):
"""
Drawing circles of a given radius around any point on earth, given the current projection.
http://www.geophysique.be/2011/02/20/matplotlib-basemap-tutorial-09-drawing-circles/
"""
glon1 = centerlon
glat1 = centerlat
X = []
Y = []
for azimuth in range(0, 360):
glon2, glat2, baz = shoot(glon1, glat1, azimuth, radius)
X.append(glon2)
Y.append(glat2)
X.append(X[0])
Y.append(Y[0])
#m.plot(X,Y,**kwargs) #Should work, but doesn't...
X,Y = m(X,Y)
plt.plot(X,Y,**kwargs)
def shoot(lon, lat, azimuth, maxdist=None):
"""Shooter Function
Plotting great circles with Basemap, but knowing only the longitude,
latitude, the azimuth and a distance. Only the origin point is known.
Original javascript on http://williams.best.vwh.net/gccalc.htm
Translated to python by Thomas Lecocq :
http://www.geophysique.be/2011/02/19/matplotlib-basemap-tutorial-08-shooting-great-circles/
"""
glat1 = lat * np.pi / 180.
glon1 = lon * np.pi / 180.
s = maxdist / 1.852
faz = azimuth * np.pi / 180.
EPS= 0.00000000005
if ((np.abs(np.cos(glat1))<EPS) and not (np.abs(np.sin(faz))<EPS)):
alert("Only N-S courses are meaningful, starting at a pole!")
a=6378.13/1.852
f=1/298.257223563
r = 1 - f
tu = r * np.tan(glat1)
sf = np.sin(faz)
cf = np.cos(faz)
if (cf==0):
b=0.
else:
b=2. * np.arctan2 (tu, cf)
cu = 1. / np.sqrt(1 + tu * tu)
su = tu * cu
sa = cu * sf
c2a = 1 - sa * sa
x = 1. + np.sqrt(1. + c2a * (1. / (r * r) - 1.))
x = (x - 2.) / x
c = 1. - x
c = (x * x / 4. + 1.) / c
d = (0.375 * x * x - 1.) * x
tu = s / (r * a * c)
y = tu
c = y + 1
while (np.abs (y - c) > EPS):
sy = np.sin(y)
cy = np.cos(y)
cz = np.cos(b + y)
e = 2. * cz * cz - 1.
c = y
x = e * cy
y = e + e - 1.
y = (((sy * sy * 4. - 3.) * y * cz * d / 6. + x) *
d / 4. - cz) * sy * d + tu
b = cu * cy * cf - su * sy
c = r * np.sqrt(sa * sa + b * b)
d = su * cy + cu * sy * cf
glat2 = (np.arctan2(d, c) + np.pi) % (2*np.pi) - np.pi
c = cu * cy - su * sy * cf
x = np.arctan2(sy * sf, c)
c = ((-3. * c2a + 4.) * f + 4.) * c2a * f / 16.
d = ((e * cy * c + cz) * sy * c + y) * sa
glon2 = ((glon1 + x - (1. - c) * d * f + np.pi) % (2*np.pi)) - np.pi
baz = (np.arctan2(sa, b) + np.pi) % (2 * np.pi)
glon2 *= 180./np.pi
glat2 *= 180./np.pi
baz *= 180./np.pi
return (glon2, glat2, baz)
print "read in etopo5 topography/bathymetry"
url = 'http://ferret.pmel.noaa.gov/thredds/dodsC/data/PMEL/etopo5.nc'
etopodata = Dataset(url)
print "get data"
def topopickle(etopodata,name):
import sys
print "\t"+name+"...",
sys.stdout.flush()
filename = "rlyeh_"+name+".pickle"
try:
with open(filename,"r") as fd:
print "load...",
var = pickle.load(fd)
except IOError:
print "copy...",
var = etopodata.variables[name][:]
with open(filename,"w") as fd:
print "dump...",
pickle.dump(var,fd)
print "ok"
return var
topoin = topopickle(etopodata,"ROSE")
lons = topopickle(etopodata,"ETOPO05_X")
lats = topopickle(etopodata,"ETOPO05_Y")
print "shift data so lons go from -180 to 180 instead of 20 to 380...",
sys.stdout.flush()
topoin,lons = shiftgrid(180.,topoin,lons,start=False)
print "ok"
# create the figure and axes instances.
fig = plt.figure()
ax = fig.add_axes([0.1,0.1,0.8,0.8])
print "setup basemap"
# set up orthographic m projection with
# perspective of satellite looking down at 50N, 100W.
# use low resolution coastlines.
m = Basemap(projection='ortho',lat_0=nemo_lat,lon_0=nemo_lon,resolution='l')
m.bluemarble()
# Generic Mapping Tools colormaps:
# GMT_drywet, GMT_gebco, GMT_globe, GMT_haxby GMT_no_green, GMT_ocean, GMT_polar,
# GMT_red2green, GMT_relief, GMT_split, GMT_wysiwyg
print "transform to nx x ny regularly spaced native projection grid"
# step=5000.
step=10000.
nx = int((m.xmax-m.xmin)/step)+1; ny = int((m.ymax-m.ymin)/step)+1
topodat = m.transform_scalar(topoin,lons,lats,nx,ny)
print "plot topography/bathymetry as shadows"
from matplotlib.colors import LightSource
ls = LightSource(azdeg = 45, altdeg = 220, hsv_min_val=0.0, hsv_max_val=1.0,
hsv_min_sat=0.0, hsv_max_sat=1.0)
# convert data to rgb array including shading from light source.
# (must specify color m)
rgb = ls.shade(topodat, cm.GMT_ocean)
im = m.imshow(rgb, alpha=0.15)
print "draw coastlines, country boundaries, fill continents"
m.drawcoastlines(linewidth=0.25)
# draw the edge of the map projection region
m.drawmapboundary(fill_color='white')
# draw lat/lon grid lines every 30 degrees.
m.drawmeridians(np.arange( 0,360,30), color="black" )
m.drawparallels(np.arange(-90,90 ,30), color="black" )
print "draw points"
psize=5
font = {'family' : 'serif',
'weight' : 'normal',
'size' : 18}
matplotlib.rc('font', **font)
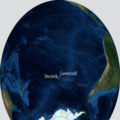
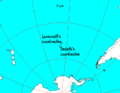
x,y = m( lovecraft_lon, lovecraft_lat )
m.scatter(x,y,psize,marker='o', color='white')
plt.text(x+50000,y+50000+50000, "Lovecraft", color='white')
x,y = m( derleth_lon, derleth_lat )
m.scatter(x,y,psize,marker='o',color='white')
plt.text(x+50000-120000,y+50000, "Derleth", color='white', horizontalalignment="right")
x,y = m( nemo_lon, nemo_lat )
m.scatter(x,y,psize*3,marker='+',color='#555555')
plt.text(x+50000+50000,y+50000-80000, "Nemo", color="#555555", verticalalignment="top")
equi(m, nemo_lon, nemo_lat, radius=2688, color="#555555" )
# x,y = m( bransfield_strait_lon, bransfield_strait_lat )
# m.scatter(x,y,psize*3,marker='+',color='#555555')
# plt.text(x+50000+20000,y+50000-80000, "bransfield_strait", color="#555555", verticalalignment="baseline")
# x,y = m( ross_sea_lon, ross_sea_lat )
# m.scatter(x,y,psize*3,marker='+',color='#555555')
# plt.text(x+50000+20000,y+50000-80000, "ross_sea", color="#555555", verticalalignment="baseline")
# x,y = m( cape_adare_lon, cape_adare_lat )
# m.scatter(x,y,psize*3,marker='+',color='#555555')
# plt.text(x+50000+20000,y+50000-80000, "cape_adare", color="#555555", verticalalignment="baseline")
plt.savefig("R'lyeh_locations.png", dpi=600, bbox_inches='tight')
# plt.show()