拉回丛
外观
(重定向自拉回叢)
数学上,拉回丛(pullback bundle)或导出丛(induced bundle)是纤维丛理论中的常见构造。令 π : E → B为以F为纤维的纤维丛,并令f : B′ → B为任意连续映射。则,f自然地诱导出一个纤维丛 π′ : f*E → B′,它也以F为纤维。大致来讲,只需要说在点x的纤维是在点f(x)的纤维就可以了;然后用不交并将所有纤维合起来。
如果要更形式化一些,可以定义
投影映射π′ : f*E → B′由下式给出
到第二个因子的投影给出了一个映射满足如下交换图:
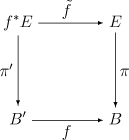
若{Ui, φi)为一E的局部平凡化,则(f−1Ui, ψi)是f*E的局部平凡化,其中
然后,f*E就是B′上以F为纤维的纤维丛了。f*E称为拉回丛或由f诱导的丛。映射是覆盖f的丛的一个态射。
若丛E → B有结构群 G,其变换函数为tij,则拉回丛f*E也有结构群G。f*E中的变换函数为
若E → B是向量丛或主丛则拉回丛f*E也是同类的丛。在主丛的情况,G在f*E上的作用为
因此,映射是右等变的,并定义了一个主丛间的态射。
用范畴论的语言,拉回丛的构造是更一般的范畴拉回的一个例子。因此,它满足相应的泛性质。
丛和层
[编辑]丛的拉回是很直接的,所以丛是本质上逆变的。与此形成对比的是,一个层是本质上协变的:其直接的构造是层的直接像。虽然每个丛都有一个截面的层,其变化是相反的。这个分歧在很多领域是一个好处。但是必须注意层的直接像相对于丛而言没有一个闭属性。取层的直接像经常可能导致产生一个不是'丛的截面'类型的新层。
因此,丛的前推的概念虽然不是没有,而且实际上很重要,但这个概念产生的对象可能在一般情况下不是丛。
参考
[编辑]- R.W. Sharpe, Differential Geometry, Springer-Verlag (1997). ISBN 0-387-94732-9
- 诱导丛(英文) (页面存档备份,存于互联网档案馆), PlanetMath







